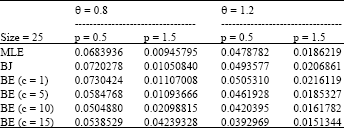
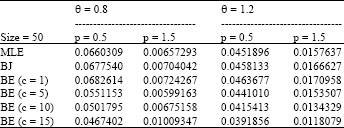
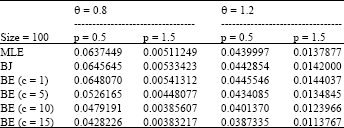
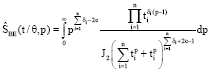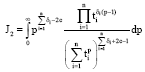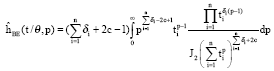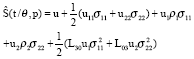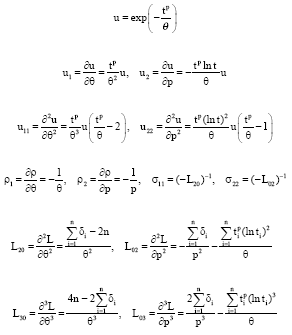Research Article
Bayesian Survival and Hazard Estimate for Weibull Censored Time Distribution
Department of Mathematics, Faculty of Science, University Putra Malaysia, 43400, Selangor, Malaysia
Noor Akma Ibrahim
Department of Mathematics, Faculty of Science, University Putra Malaysia, 43400, Selangor, Malaysia
Mohd Bakri Adam
Department of Mathematics, Faculty of Science, University Putra Malaysia, 43400, Selangor, Malaysia
Jayanthi Arasan
Department of Mathematics, Faculty of Science, University Putra Malaysia, 43400, Selangor, Malaysia