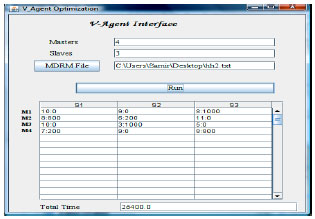
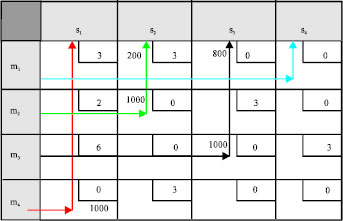
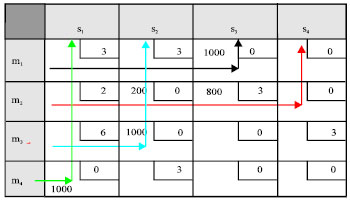
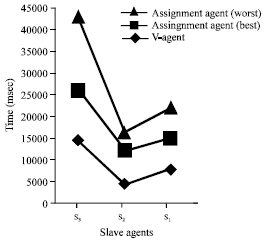
Research Article
Evaluating Time Performance Optimization Analysis for Mobile Agent Message Communication Using Assignment Computing Agent
Faculty of Information Technology, Applied Science University, Amman, 11931, Jordan
Hesham Abusaimeh
Faculty of Information Technology, Applied Science University, Amman, 11931, Jordan
Khalil Al Shqeerat
Faculty of Information Technology, Applied Science University, Amman, 11931, Jordan
Mahmoud Omari
Faculty of Information Technology, Applied Science University, Amman, 11931, Jordan