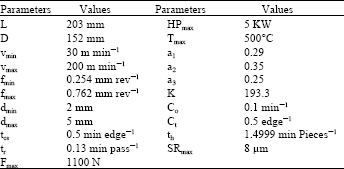
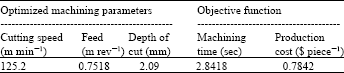
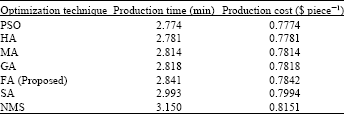
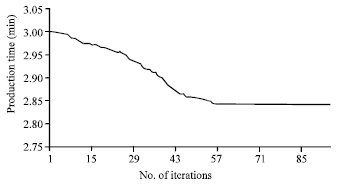
Research Article
Optimization of Constrained Machining Parameters in Turning Operation Using Firefly Algorithm
School of Mechanical Engineering, SASTRA University, Thanjavur-613 401, Tamil Nadu, India
N. Sathiya Narayanan
School of Mechanical Engineering, SASTRA University, Thanjavur-613 401, Tamil Nadu, India
C.V. Srinivas Pramod
School of Mechanical Engineering, SASTRA University, Thanjavur-613 401, Tamil Nadu, India
Arvind Ragunathan
School of Mechanical Engineering, SASTRA University, Thanjavur-613 401, Tamil Nadu, India
Somala Raju Vinesh
School of Mechanical Engineering, SASTRA University, Thanjavur-613 401, Tamil Nadu, India
K. Vamshee Krishna
School of Mechanical Engineering, SASTRA University, Thanjavur-613 401, Tamil Nadu, India