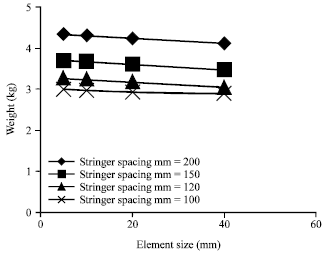
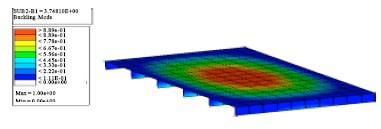
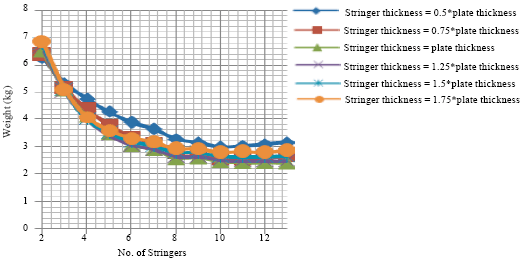
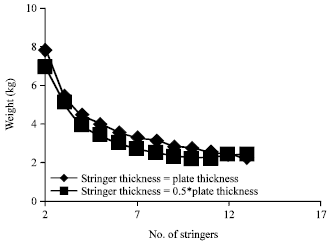
Research Article
Effect of Ribs and Stringer Spacings on the Weight of Aircraft Structure for Aluminum Material
Department of Mechanical Engineering, Vidyavardhaka College of Engineering, 570002, Mysore, India
N. Lohith
Department of Aerospace Laboratory, National Aerospace Laboratories, Bangalore, India
B.B. Ganesha
Department of Mechanical Engineering, Vidyavardhaka College of Engineering, 570002, Mysore, India