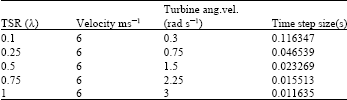
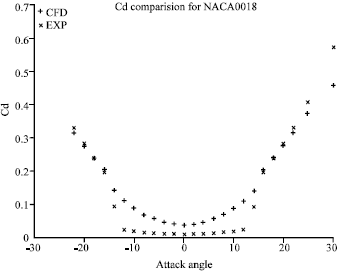
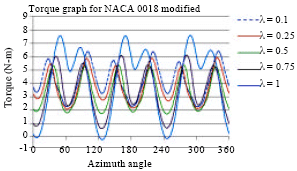
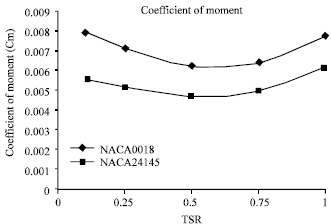
Research Article
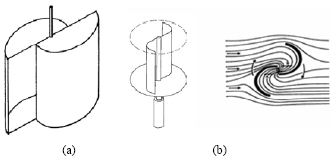
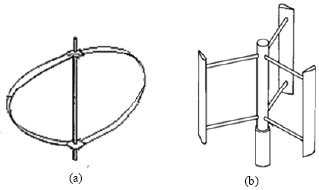
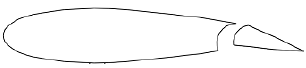
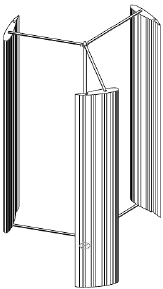
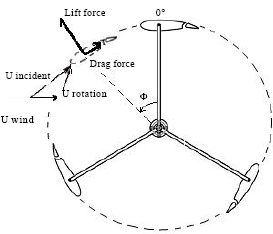
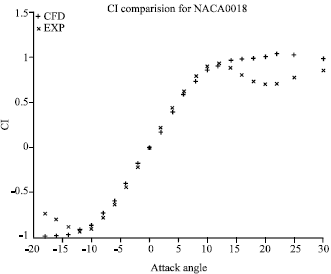
Numerical Simulation of Unsteady Flow to Show Self-starting of Vertical Axis Wind Turbine Using Fluent
Department of Manufacturing and Automation, Harbin Institute of Technology, Harbin, 150001, China
Yingxue Yao
Department of Manufacturing and Automation, Harbin Institute of Technology, Harbin, 150001, China