Research Article
Systematic Minimization Technique for Majority-Majority Digital Combinational Circuits
Department of Computer Science, College of Computer and Information Sciences, King Saud University, Saudi Arabia
The Quantum Cellular Automata (QCA) was first projected in 1993, unlike standard computers in which information is transferred from one place to another by means of electrical current, QCA transfers information by propagating a polarization state (Zhang et al., 2004; Toth and Lent, 2000; Orlov et al., 2003), QCA is based on the encoding of binary information in the charge arrangement within the quantum dot cells. Computational power is provided by the Coulombic interaction between QCA cells (Graunke et al., 2005). The interconnections between the cells are provided by the physics of cell-to-cell interaction due to the reorganization of electron positions (Toth and Lent, 2000). Tentative experimental results signified that QCA may be an extremely feasible option to CMOS. QCA cells and QCA logical devices have been efficiently fabricated and tested (Zhirnov et al., 2003). Nevertheless, a systematic methodical for constructing and designing QCA circuits are crucial for the development in this field. Essential logical devices and an adder have been designed by Bhanja and Sarkar (2006). Such devices were simulate with a simulation software called AQUINAS. Memory has been studied by Toth and Lent (1999) and a complex SRAM cell has undergone successful simulation. Furthermore, a simple shift register has also been constructed and simulated (Zhirnov et al., 2003). Both of these design schematics take advantage of architecture developed by the authors (Toth and Lent, 1999), called the SQUARES architecture. The SQUARES architecture essentially consists of cells that are 5 QCA cells wide and 5 QCA cells high. A library of different QCA well-designed devices such as a majority gate was then built up (with each device\housed" in a square) and used to build the various schematics. This technique resulted in successful simulations. The shortcoming to the SQUARES structural design was that designs using it had less than optimal density (Bhanja and Sarkar, 2006). Previous work on the QCA architecture was about studying QCA cells. The few accessible QCA logical circuit designs such as the adder, XOR gate and multiplexor, using the QCA the majority gate, were designed and studied. For many QCA circuits simplified versions could be constructed with QCA majority gates. It would be exceptionally valuable to create a CAD tool that could translate a schematic containing conventional Boolean logic equations into a schematic consisting entirely of QCA majority gates. Some accessible tools such as Mentor Graphics' AutoLogic II achieve this task. It allows a schematic created with general library components to be mapped to a specific technology provided that a library for that technology exists. The intention was to create such a QCA library with the hope that, once completed, this tool would take as input any conventional schematic, Boolean equation, or VHDL code and generate its minimized equivalent in QCA. An important comprehension of the lack of a complete set of QCA design rules is essential for a complete and thorough CAD program. As QCA is being investigated as an alternative to CMOS, an ultimate goal should be to build complete microcomputers from QCA cells. This will not be viable without a systematic way to manufacture and minimize logic functions in a paradigm suitable for QCA. This is the main contribution of this research. In this paper a J-Map for the realization and minimization of logic functions in terms of majority logic function is invented. Also, generalization of the J-Map for n variable logic functions will be introduced.
QUANTUM-DOT CELLULAR AUTOMATA
Quantum-dot Cellular Automata (QCA) are a computational nanotechnology. It is based on a the basic QCA device QCA cell composed of four quantum dots arranged in a square pattern as shown in Fig. 1. Four quantum dots are situated to form a square (Srivastava and Bhanja 2007). Quantum dots are small semi-conductor islands with a diameter that is small enough to make their charging energy greater than kBT (where kB is Boltzmann's constant and T is the operating temperature). Precisely two mobile electrons are loaded in the cell and can stir to different quantum dots in the QCA cell by means of electron tunneling. The lines connecting the quantum dots in Fig. 1 represent tunneling paths. Coulombic repulsion will originate the electrons to occupy only the corners of the QCA cell resulting in two specific polarizations. The cell is charged with two excess electrons, which can be permitted, to tunnel between the different quantum dots by a clocking mechanism. These electrons tend to occupy diagonally opposed dots due to their Coulomb force repulsion. The Coulomb force repulsion is also accountable for the transfer of information from one cell to an adjacent cell.
For an isolated cell there are two energetically minimal equivalent arrangements of the two electrons in the QCA cell denoted cell polarization P = +1 and cell polarization P = -1. Cell polarization P = +1 represents a binary 1 while cell polarization P = -1 represents a binary 0. Quantum-dot Cellular Automata (QCA) uses majority gate as a fundamental logic primitive.
When five QCA cells arranged in a cross pattern, they form a majority gate as shown in Fig. 2. The fundamental QCA logical circuit is the three-input majority gate. Computation will be performed with the majority gate by driving the device cell (central cell in Fig. 2) to its lowest energy state.
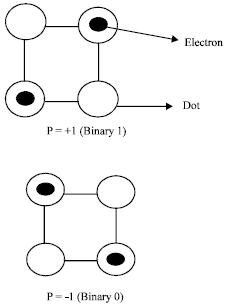 | |
| Fig. 1: | QCA cell polarizations and representations of binary 1 and binary 0 |
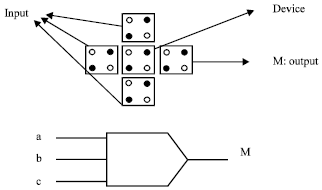 | |
| Fig. 2: | Majority gate consists of five quantum dots |
This happens when it assumes the polarization of the majority of the three input cells. The device cell will always assume the majority polarization because it is this polarization where electron repulsion between the electrons in the three input cells and the device cell will be at a minimum.
THE PROPOSED NEW MINIMIZATION TECHNIQUE
In this study, a new technique for realization and minimization of logic functions in the form of Majority of majority functions. To obtain our reduction, we first create the K-Map corresponding to the Boolean function we intend to represent. Then, in each cell that has a Boolean 1 value we rename it 11-. The cell with Boolean 0 will be given the value 00-. This will produce a new K-Map that will be pointed to as J-Map denoting majority function logic minimization map that mimics K-Map but instead minimizing functions to the AND-OR plane, it minimized in to the Majority of Majority plane.
 | |
| Fig. 3: | T shape that represent a majority function M (a’, b, c) = a’b+bc+ca’ |
 | |
| Fig. 4a: | K-Map of a Boolean function, F = a’b’c+ a’bc’+abc+abc’ |
 | |
| Fig. 4b: | J-Map of a Boolean function F = a’b’c+ a’bc’+abc+abc’ |
We then express the Boolean in function in terms of majority of majority functions. Minimization of such function will result in a majority function of majority functions: M (M1, M2, M3).
Minimization of M will be done on the J-Map by obeying the following rules:
| • | Cover any “11-” at least twice |
| • | Cover a “00-” at most once |
| • | The covering of the terms in the J-Map is the same as in the K-Map such as covering adjacent minterms as much as you can as long as their number are in the form 2n |
| • | Cover the minterms in the form of T shape that represent a majority function |
| • | Overlapping is allowed, as long as rules 1 and 2 are enacted |
We now demonstrate the application of this method to various Boolean functions. In Fig. 3, the T shape that represent a majority function M (a’, b, c) = a’b+bc+ca’ is represented. The K-Map and J-Map of the Boolean function F = a’b’c+a’bc’+abc+abc’ is shown in Fig. 4a, b.
The innovative minimization J-Map algorithm can produce different minimized logic functions, its output is not unique it just like K-Map it produces the minimized function with the minterms covering as shown in Fig. 5, where the steps of the minimization of the function F is described and the minimized function is: F = M (M (a’, b, c), M (a’, b, c’), M (0, b, c’)) (Fig. 5d).
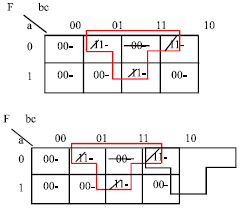 | |
| Fig. 5a: | Step 1 of the minimization of the Boolean function F = a’b’c+a’bc’+abc+abc’ |
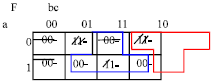 | |
| Fig. 5b: | Step 2 of the minimization of F = a’b’c+ a’bc’+abc+abc’ |
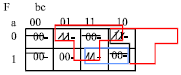 | |
| Fig. 5c: | Step 3 of the minimization of F = a’b’c+ a’bc’+abc+abc’ |
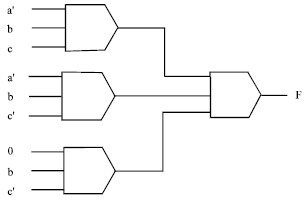 | |
| Fig. 5d: | The steps of the minimization of F F = M (M (a’, b, c), M (a’, b, c’), M (0, b, c’)) |
DESIGN OF A FULL-ADDER CELL IN QCA PARADIGM
In this study, we are going to design a full adder cell built in QCA model. We are Considering the computation of the sum of a full-adder.
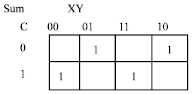 | |
| Fig. 6a: | The K-Map for the sum logic function of the full adder Sum |
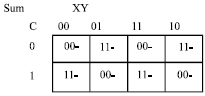 | |
| Fig. 6b: | The J-Map for the full adder Sum |
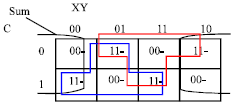 | |
| Fig. 6c: | The J-Map for the Sum= M (M (X, Y’, C), M (X’Y’C), C’) |
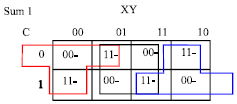 | |
| Fig. 6d: | The full adder Sum Sum1 = M ((M (X, Y, C))’, M (X, Y, C’), C) |
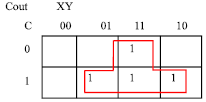 | |
| Fig. 6e: | J-Map minimization of the function Cout = XC+XY+YC |
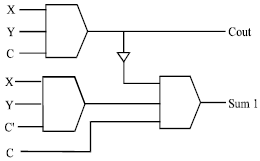 | |
| Fig. 6f: | Schematic diagram for the full adder Sum1 and Cout |
It will be represented in the K-Map as shown in Fig. 6a. While the utilization of the J-Map technique on the Sum function is depicted in Fig. 6b-d. The minimization of the carry-out function is depicted in Fig. 6e.
The realization of the full adder cell using minimization depicted in Fig. 6d. will require three majority functions and an inverter as depicted in Fig. 6f.
NEW ADDER DESIGN WITH FEWER QUANTUM DOTS
In this study, we are going to introduce a new adder design that can minimize the number of quantum dots required to realize the n-bit propagation adders.
| (1) |
| (2) |
Equation 2 can be arranged as follows:
| (3) |
| (4) |
The ripple carry adder will be realized by Eq. 1 and 4. Cell1 in the ripple adder will start y inverting Cin and it will produce S and Cout’. The rest of the cells is realized using the previous Cout’ as the Cin’. The last cell in the ripple carry adder will invert its Cout’ to the final Cout.
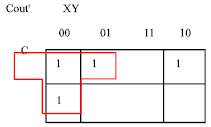 | |
| Fig. 7a: | The minimized J-Map for the Cout’=M (X’, Y’, C’) |
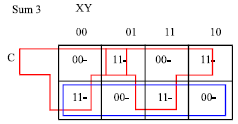 | |
| Fig. 7b: | The minimized J-Map for Sum3 |
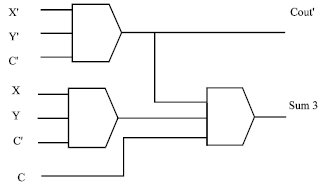 | |
| Fig. 8: | Schematic diagram for the full adder Sum3 and Cout’ |
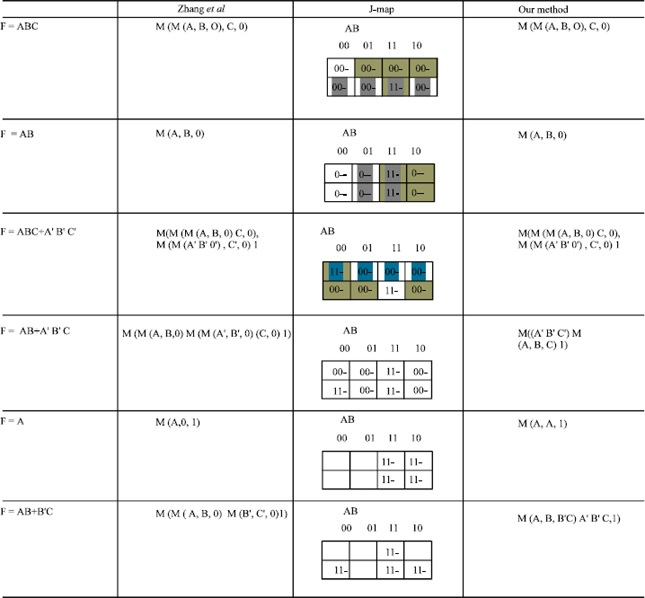
| Table1: | Implementation on diffrent gates using our methodology |
 | |
The majority gate realization is depicted in Fig. 7 and 8.
RESULTS AND DISCUSSION
In this study, we are comparing our methodology to the technique demonstrated by the authors in (Zhang et al., 2004). We minimized all the 13 functions that the authors demonstrated in their paper. The comparison is depicted in Table 1, where it can be concluded that our technique is producing the same results but with some advantageous features, the first feature is the ease of use of J-Map and the second feature is that J-Map can give alternative solutions if more than one exists. The third and most important feature is that J-Map constitutes a basis for Algebra based on majority of majority minimization. The fourth feature is that the J-Map technique can be expanded to more than three variables.
XJ-MAP: PROPOSED EXTENDED PROCEDURE TO BUILD MAJORITY EXPRESSIONS
Here, we suggest an extended procedure method to build simplified majority expressions for a given Boolean function using J-Map. The method uses the subsequent algorithm to produce a majority gate expression of the three-variable Boolean function.
| Algorithm 1: | XJ-Map |
 | |
| Algorithm 2: | Construct XJ-Map |
 | |
An Example of XJ-Map will be depicted by executing the minimization of the following function:
F = ABC + A’B’C’. |
The corresponding J-Map is depicted in Fig. 9a. There are four covering comprising the minimal cover. The two covers, B and A are overlapped, but not overlapped with the other covers. The other two covers A′B′C′ and A′B′C′ are overlapped together, but not with the first two covers. Therefore, we have to extend the technique to use the XJ-Map technique. This J-Map will be divided into two j maps, that are depicted in Fig. 9b. The minimization of the XJ-Map will be the minimization of each J-Map separately, then the Majority of at most three j maps together are combined to form nested Majority of Majority functions.
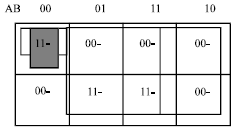 | |
| Fig. 9a: | J-Map of F = ABC+A’B’C’ |
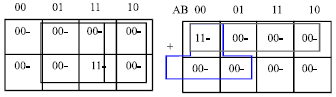 | |
| Fig. 9b: | XJ-Map of executing the minimization of the following function: F = ABC+A’B’C’ |
The minimum cover will be as follows: M(M(A,B,0), M(C’,M(A’B’C), 0),1)
EXTENSION TO FOUR AND FIVE VARIABLES BOOLEAN FUNCTIONS
We are going to extend XJ-Map for 4 and 5 variables Boolean functions.
Algorithm 3: | XJ-Map4-5 variables |
 | |
Algorithm 4: | Construct XJ4-5map |
 | |
An Example of XJ4-5map will be depicted by executing the minimization of the following function: F=ABCD+A’B’C’
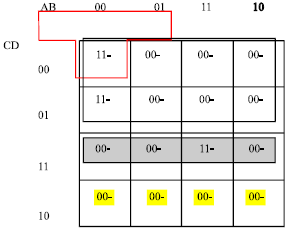 | |
| Fig. 10a | :J4-5map executing the minimization of the following function: F = ABCD+A’B’C’ |
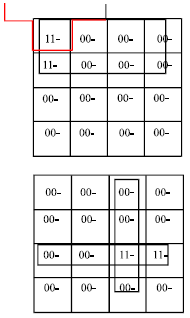 | |
| Fig. 10b: | XJ4-5map The final solution will be as follows: F = M (C’, M (A’B’D’), 0), M (AB,CD,0), 1) |
The originated J4-5 map and the corresponding XJ-4 map are depicted in Fig. 10. The final solution will be as follows:
F=M (C’, M (A’B’D’), 0), M (AB, CD, 0), 1) |
The QCA logic circuits that are shown in Fig. 6, 8 and 9 were simulated using QCAD esigner. The simulation procedure is depicted in the following steps as defined in (Zhang et al., 2004).
Steps:
| • | The first step is to generate the layout of the QCA circuit |
| • | The second step is to setup the circuit clocking |
| • | The third step is to set up the vector table simulation to simulate the circuit |
The QCA cells are made of 2 nm quantum dots. The cells are separated by 10 nm. This design requires only 36% of the area used by the original design f these circuits withut the Majority of Majority minimization techniques. While maintaining the same clocking performance. Also the design for the gates in Fig. 6 and 9 achieved decrease in area by 40 and 35% from the original designs. The decrease in area requirement is consistent with the theoretical reasoning.
CONCLUSION
This research is an effort to investigate the potential of a nanotechnology (QCA) as being a viable alternative to CMOS VLSI. In this study we are concentrated particularly on logic design issues. Namely, a solution for potential systematic extensible technique for QCA logic realization and minimization was developed. Most importantly, this solution can be applied and scaled to more complicated designs. Emerging technologies specifically, Quantum-dot Cellular Automata (QCA) uses majority gate as a fundamental logic primitive instead of the AND-OR combination gates. We report an intuitive systematic methodology J-Map minimization technique for reduction of 3-variable Boolean functions into a simplified majority representation. The main contribution of this work is the general and systematic way the new approach can be applied. All attempts in the literature were complex and lacked the systematic approach we are offering (Toth and Lent, 2000).