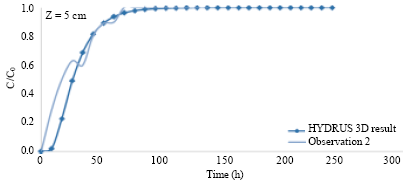
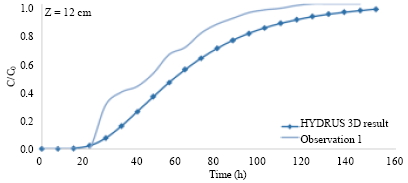
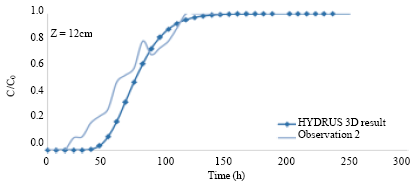
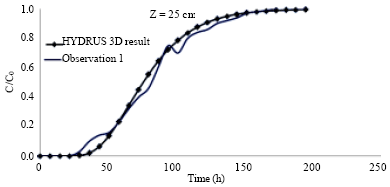
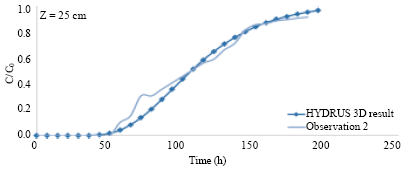
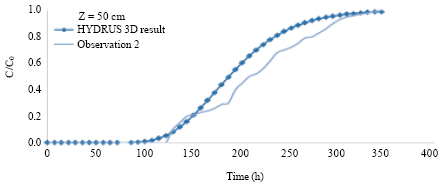
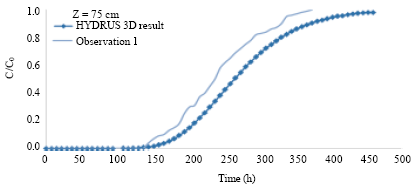
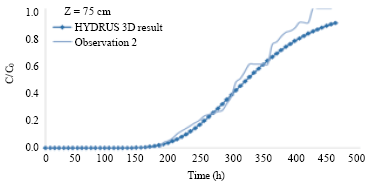
Research Article
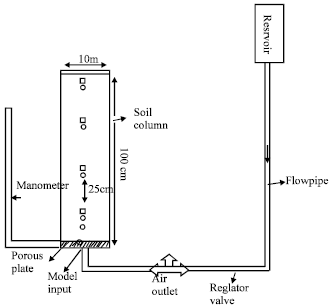
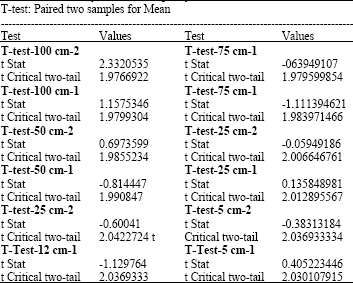
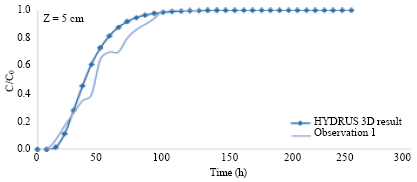
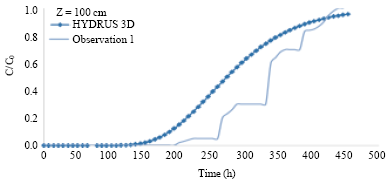
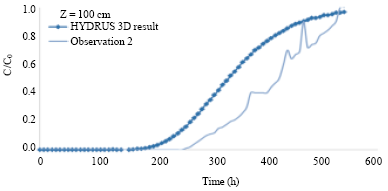
Phosphorus Transport Through a Saturated Soil Column: Comparison Between Physical Modeling and HYDRUS-3D Outputs
Department of Irrigation and Drainage, Chamran University, Ahvaz, Iran
Y. Hoseini
Department of Irrigation and Drainage, Chamran University, Ahvaz, Iran
H. Moazed
Department of Irrigation and Drainage, Chamran University, Ahvaz, Iran
F. Abbasi
Agricultural Engineering Research Institute, AERI, P.O. Box 31585-845, Karaj, Iran
H. M. V. Samani
Department of Irrigation and Drainage, Chamran University, Ahvaz, Iran
S. A. Sakebi
Soil and Water Consulting Engineers, Ahvaz, Khuzestan, Iran