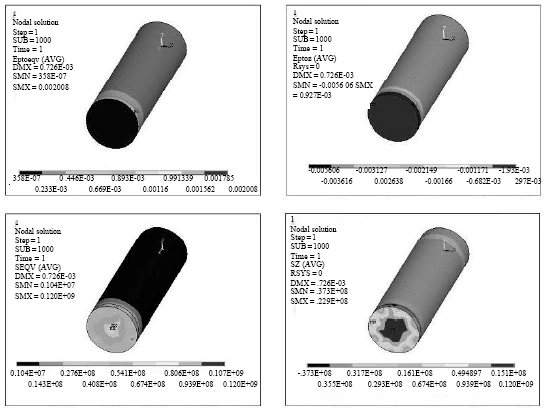
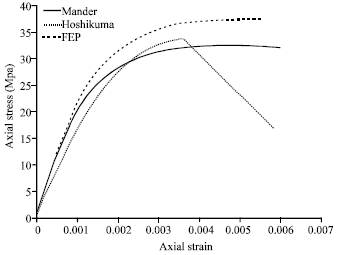
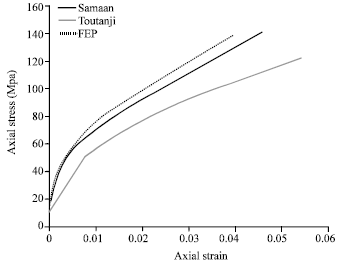
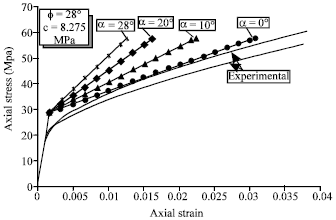
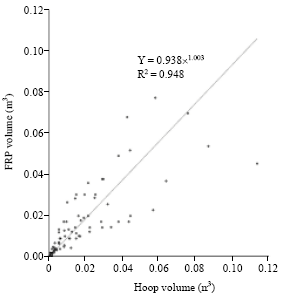
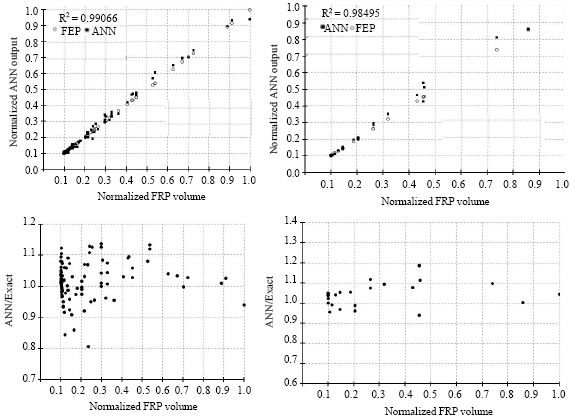
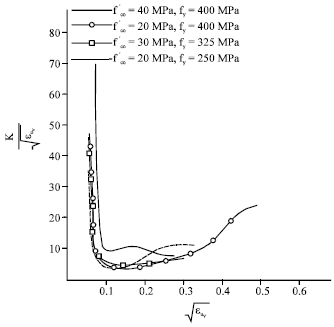
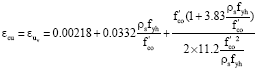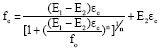Research Article
FRP-Steel Relation in Circular Columns to Make an Equal Confinement
Behbahan Higher Educational Complex, Iran
A. Amani
Department of Civil Engineering, Tarbiat Modares University, Iran
S. Motaghed
Behbahan Higher Educational Complex, Iran