Research Article
The Performance of Robust Multivariate Statistical Control Charts based on Different Cutoff-points with Sustained Shift in Mean
Laboratory of Applied and Computational Statistics, Institute for Mathematical Research, University Putra Malaysia, 43400 Serdang, Selangor, Malaysia
Habshah Midi
Department of Mathematics, Faculty of Science, University of Putra Malaysia, 43400 Serdang, Selangor, Malaysia
Mohd Nooh Hassan
Department of Mathematics, Faculty of Science, University of Putra Malaysia, 43400 Serdang, Selangor, Malaysia









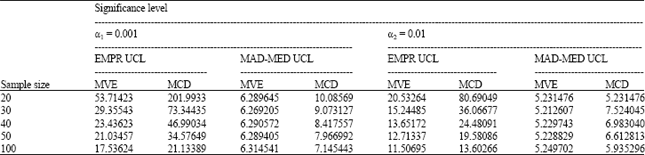
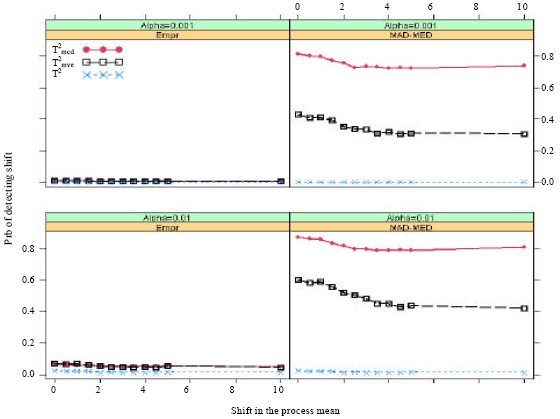
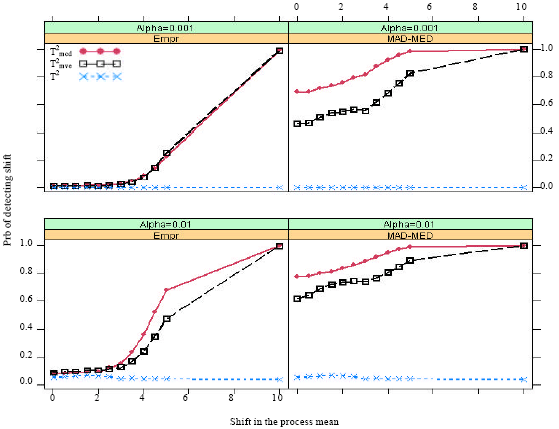
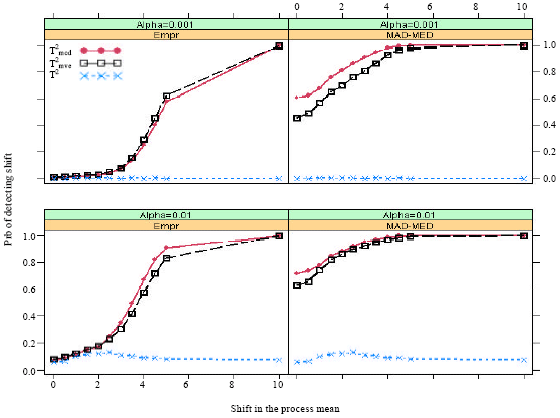

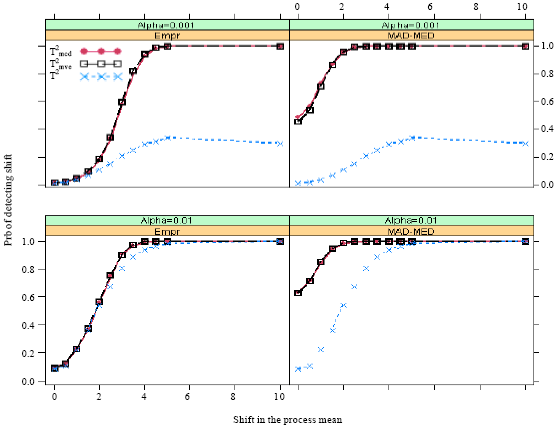
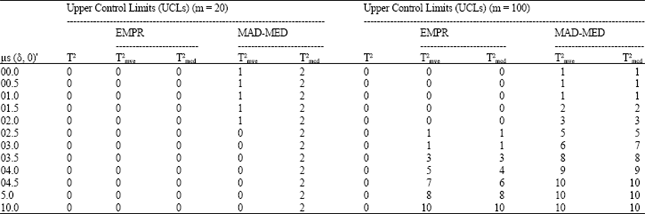
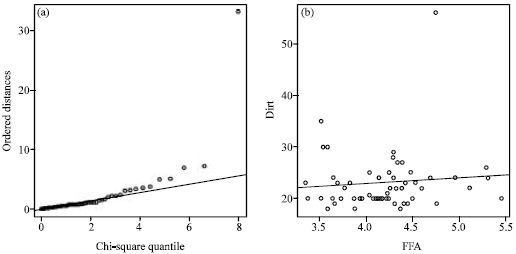
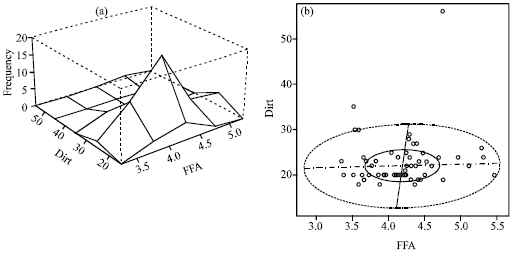

marzieh Reply
It is an excellent article. It was useful in my research