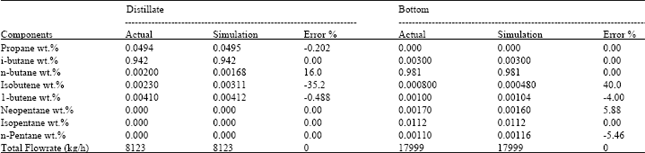
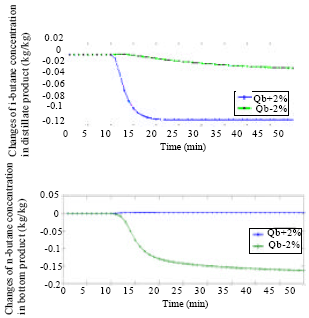
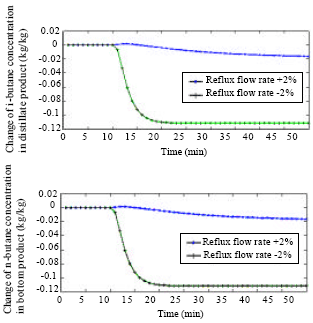
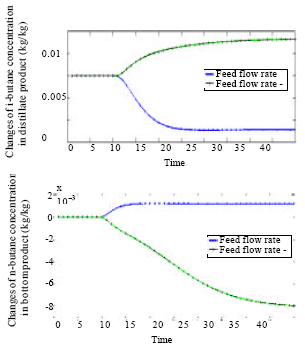
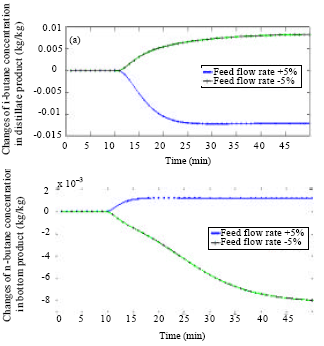
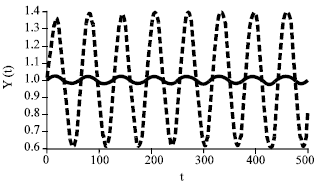
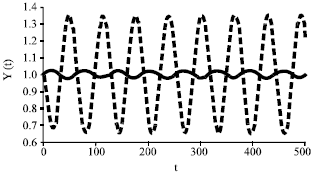
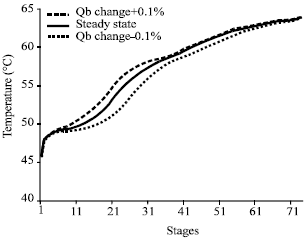
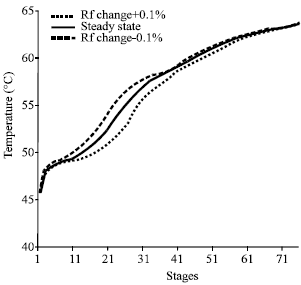
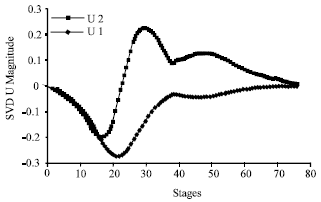
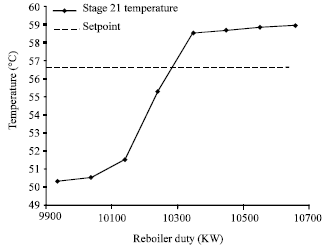
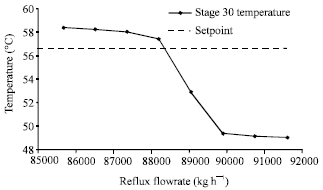
Research Article
Modeling and Nonlinearity Studies of Industrial i-Butane/n-Butane Distillation Column
School of Chemical Engineering, Engineering Campus, Universiti Sains Malaysia, Seri Ampangan 14300 Nibong Tebal, Seberang Perai Selatan, Penang, Malaysia
Z. Ahmad
School of Chemical Engineering, Engineering Campus, Universiti Sains Malaysia, Seri Ampangan 14300 Nibong Tebal, Seberang Perai Selatan, Penang, Malaysia
N. Aziz
School of Chemical Engineering, Engineering Campus, Universiti Sains Malaysia, Seri Ampangan 14300 Nibong Tebal, Seberang Perai Selatan, Penang, Malaysia