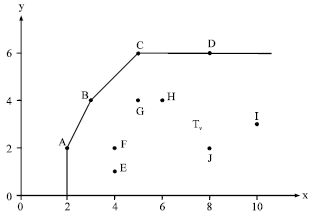
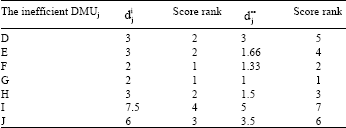
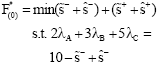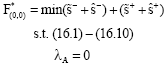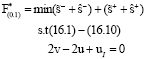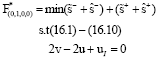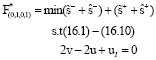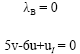Research Article
An Approach using a Branch-and-Bound Algorithm for Evaluating the Performance of Inefficient DMUs in DEA
Faculty of Mathematical and Computer Sciences, Teacher Training University, 599 Taleghani Avenue, 15618 Tehran, Iran
J. Vakili
Faculty of Mathematical and Computer Sciences, Teacher Training University, 599 Taleghani Avenue, 15618 Tehran, Iran
S. M. Mirdehghan
Faculty of Mathematical and Computer Sciences, Teacher Training University, 599 Taleghani Avenue, 15618 Tehran, Iran