Research Article
Estimation Parameters of Weighted Exponential Distribution with Presence of Outliers Generated from Exponential Distribution
Department of Statistics, Payame Noor University, P.O. Box 19395-3697, Tehran, Iran
P. Nasiri
Department of Statistics, Payame Noor University, P.O. Box 19395-3697, Tehran, Iran









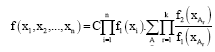
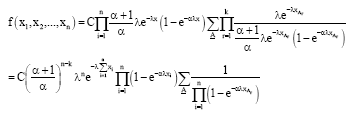
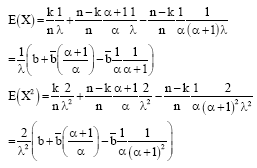
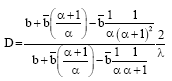
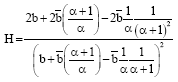
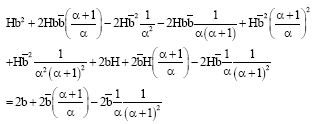
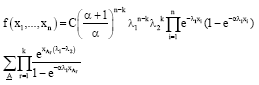


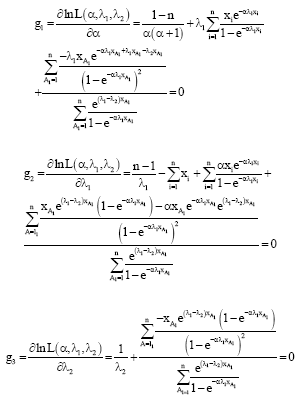

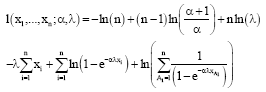
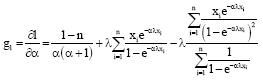
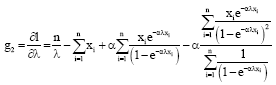
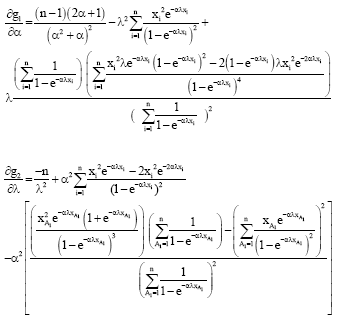
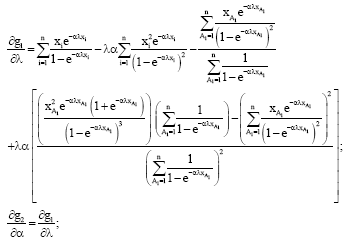
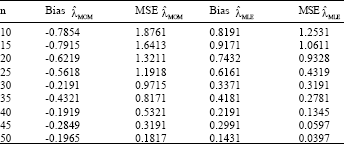
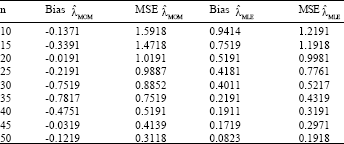
Parviz Nasiri Reply
I need one copy of this paper.
Thanks