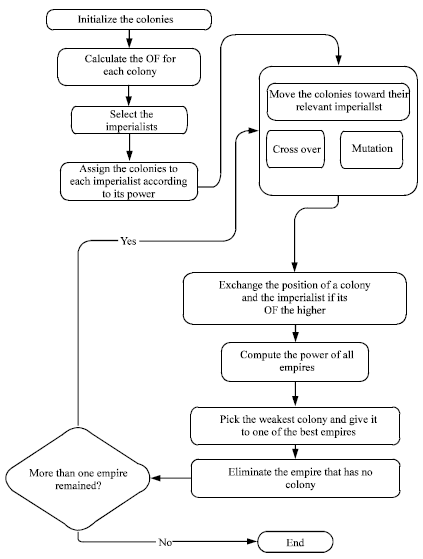
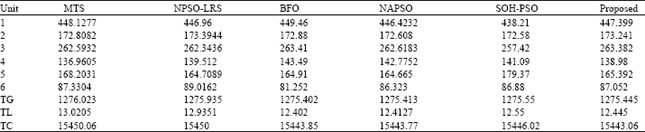
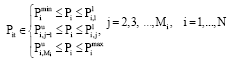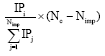Research Article
A New Heuristic Algorithm for Solving Non-convex Economic Power Dispatch
Department of Engineering, Abhar Branch, Islamic Azad University, Abhar, Iran
S. Mobaieen
Department of Engineering, Abhar Branch, Islamic Azad University, Abhar, Iran
B. Mohamady
Department of Engineering, Abhar Branch, Islamic Azad University, Abhar, Iran
A. Suroody
Department of Engineering, Abhar Branch, Islamic Azad University, Abhar, Iran