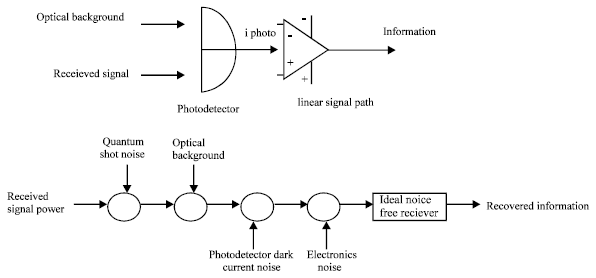
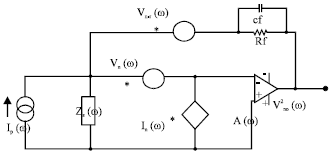
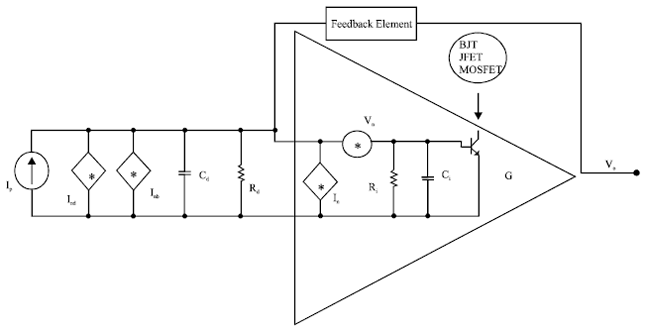
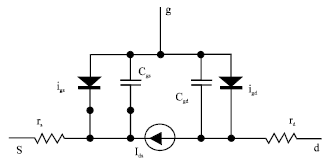
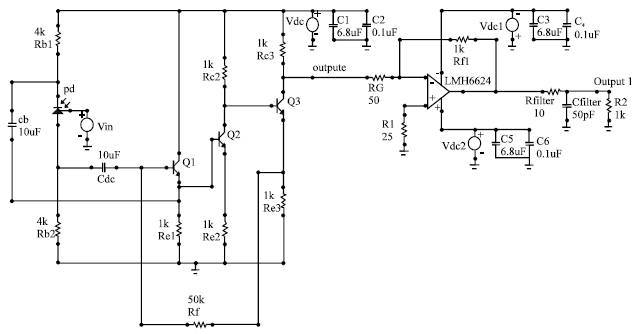
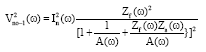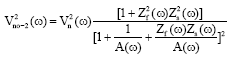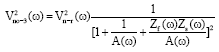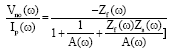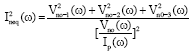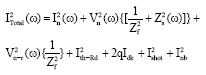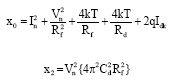Research Article
Noise Analysis Adjustable Bootstrap Transimpedance and Voltage Feedback Receiver Amplifier
Department of Communication Engineering, Faculty of Electrical and Electronic Engineering, University Tun Hussein Onn Malaysia, 86400 Parit Raja, Batu Pahat, Johor, Malaysia
R.J Green
School of Engineering, University of Warwick, United Kingdom