ABSTRACT
Two variations of N-point Central Composite Designs (CCDs) which are either orthogonally or rotatably restricted are compared. The basis of variation in these designs is the common distance of the axial points from the center of the design. Using the D-optimality criterion, it is concluded that replicated cubes plus one star variation is preferable to the replicated stars plus one cube variation under both restrictions.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2011.3732.3737
URL: https://scialert.net/abstract/?doi=jas.2011.3732.3737
INTRODUCTION
It is sometimes desirable to replicate the points in a design. This will allow the experimenter to later estimate the pure error in the experiment. Many authors have discussed the analysis of such experiments (Cochran and Cox, 1957; Montgomery, 1991; Atkinson and Donev, 1992). However, it should be clear that, when replicating the design points, the experimenter could compute the variability of measurements within each unique combination of factor levels. This variability will give an indication of the random error in the measurement because the replicated observations are taken under identical conditions. Such an estimate of the pure error can be used to evaluate the size and statistical significance of the variability that can be attributed to manipulated factors (Box and Draper, 1987). It may not be possible to replicate each unique combination of factor levels, that is, the full design, but the experimenter can still gain an estimate of pure error by replicating only some of the runs (points) in the design. In this case of partial replications, the experimenter faces the problem of choosing the points to be replicated and the points not to be replicated in the design.
In this study, specific interest is centered on the Central Composite Designs (CCDs) which are the most practically useful class of second-order designs and one of many experimental designs where partial replication is applicable. Since the best design option is sought, we shall hover around the restricted CCD (which is a CCD with restrictions such as orthogonality, rotatability, etc., imposed on it). It has been shown in Nwobi et al. (2001) that, with designs, restrictions involving orthogonality or rotatability or even both orthogonality and rotatability is better (in the sense of smaller variance) than the unrestricted. A CCD consists of a 2K factorial or a 2K-q fractional factorial portion (run), usually called a cube, with points selected from the 2K points (x1, x2,..., xk) = (±1, ±1,..., ±1) usually of resolution V or higher, plus a set of 2K axial points (runs) at a distance α from the origin, usually called a star, plus one or more center points. In general, the cube and star may be replicated also (Draper, 1982; Draper and Lin, 1990). Thus, we have a total of N (= 2K n1+2Kn2+n0) points where n1 is the number of cubes; n2 is the number of stars and n0 is the number of center points. Typically, the value of α will be chosen to satisfy the property of orthogonality or rotatability (Draper and John, 1998). More so, CCDs are extremely useful for sequential experimentation in which the cube portion is used to allow for estimation of the first-order effects, the later addition of the star points permits second-order terms to be added to the model and estimated. Although cube and star portions are used at different stages and purposes, it is plausible to know the portion of a restricted CCD to be replicated when it is not possible to replicate all points equally, because of the reason mentioned earlier. Box and Hunter (1957) has pointed out that the variance of estimate can be reduced by increasing N, the number of experiments (e.g., by replicating the points); see also Box and Draper (1982). An attempt to break this dilemma is made in this study. The two variations of restricted CCD that will arise which are replicated cubes plus one star and replicated stars plus one cube are compared. The variations are distinguished by the value of α only.
Our approach to this study is to express the information matrix of a restricted CCD in terms of numbers of cubes and stars and then find out the desired portion, which optimizes the design under consideration. The D-optimal design criterion, which maximizes the determinant of the information matrix of a design, is employed for the comparison in this work. This is so because it has been proved by Nalimov et al. (1970) that the D-optimum concept can be used as the theoretical basis for building and comparing response surface designs in use.
CENTRAL COMPOSITE DESIGNS
The CCD is the 2K factorial or a 2K-q fractional factorial design with the levels of each factor coded to the usual -1, +1, augmented by the following points: (±α, 0, ..., 0), (0, ±α, ..., 0) (0, 0, ... ,±α) and (0, 0, ..., 0). The experimenter according to some restrictions such as orthogonality or rotatability selects the value of α. In order to show how these restrictions are made in choosing α, attention will be paid to the expanded design matrix, X and the information matrix, X’X, for the general CCD.
Orthogonal restriction: Consider the response surface, say = φ(x1, x2,..., xk) represented in the experimental area, [±α, ±1], by the quadratic function:
| (1) |
where, yj and ej are, respectively the response and the random error of the jth observation; β00, βi0, βii and βii are the unknown parameters of the regression model and x1, x2,..., xk are the independent variables. Alternatively, in vector notation, (1) is given by:
| (2) |
where, Y and e are the, respective (Nx1) response and error column vectors; ![]() is an (NxP) matrix of independent variables of rank P; β is the (Px1) column vector of the unknown parameters. From (1), we obtain the average:
is an (NxP) matrix of independent variables of rank P; β is the (Px1) column vector of the unknown parameters. From (1), we obtain the average:
| (3) |
By subtracting Eq. 3 from Eq. 1, we obtain:
| (4) |
where, ![]() and
and ![]() .
.
Recall from Eq. 1, that:
hence, ![]() . Then, (2) becomes:
. Then, (2) becomes:
| (5) |
after subtracting Eq. 3 from it, where ![]()
![]() and:
and:
 | (6) |
is the {Nx(P-1)} design matrix; N = 2Kn1+2Kn2+n0,
1 = (1, 1, ..., 1)' is a 2Kn1/4 component vector, ![]() is of n2 components, α2 = (α2, α2,..., α2) 01 = (0, 0, ..., 0) is of n2 components 02 = (0, 0, ..., 0) is of (K-2)n2 components, 03 = (0, 0,...., 0) is of n0 components. The information matrix of the design is obtained as:
is of n2 components, α2 = (α2, α2,..., α2) 01 = (0, 0, ..., 0) is of n2 components 02 = (0, 0, ..., 0) is of (K-2)n2 components, 03 = (0, 0,...., 0) is of n0 components. The information matrix of the design is obtained as:
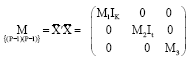 | (7) |
where, M1 is the sum of squares of the elements in the vectors associated with the first-order terms while M2 is the sum of squares of the elements in the vectors associated with the two-way cross-product terms. However, M3 is a (KxK) matrix whose diagonal elements (denoted by p) are the sums of squares of the elements in the vectors associated with the adjusted second-order terms and also, whose off-diagonal elements (denoted by q) are the sums of cross-products of the elements in the vectors associated with the adjusted second-order terms. Using notations accordingly, M1 = 2K n1+2n2α2, M2 = 2K n1 and M3 = (p-q)IK+qJK. Note that, IK is an (KxK) identity matrix, It is an (txt) identity matrix; where:
and Jk = 11, 1 is a column vector of K components. Using Eq. 6, we obtain;
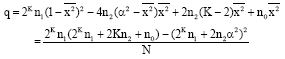 | (8) |
| (9) |
where:
Having obtained ![]() and
and ![]() , the definition of orthogonally-restricted CCD is given below.
, the definition of orthogonally-restricted CCD is given below.
Orthogonally-Restricted CCD: A CCD is orthogonally-restricted if ![]() has a diagonal structure, that is, if and only if q = 0 in M3 of Eq. 7.
has a diagonal structure, that is, if and only if q = 0 in M3 of Eq. 7.
Rotatable restriction: The concept of rotatability was first introduced by Box and Hunter (1957) and has since become an important design criterion. The important feature of rotatability is that the quality of variance of prediction of the response denoted by V[í(x)] is invariant to any rotation of the coordinate axes in the space of the input variables (Khuri, 1988). A succinct characterization of ratability is given in terms of the elements of ![]() . These elements are known as design moments although, originally, the elements of:
. These elements are known as design moments although, originally, the elements of:
are referred to as design moments (Khuri, 1988). One the whole, a design moment for a model such as the one given in Eq. 1 of order d (d = 2)and in K input variables is denoted by (1δ1 2δ2 ... KδK) and is given by:
| (10) |
where, ![]() are nonnegative integers. The sum:
are nonnegative integers. The sum:
is called the order of the design moment and is denoted by δ (δ = 0, 1, ...,2d). For example, (11 31 53) is a design moment of order δ = 5Δ and is equal to
A necessary and sufficient condition for a design for fitting a model such as that of (1) to be rotatable is that the design moments of δ (δ = 0, 1, ...,2d) be of the form:
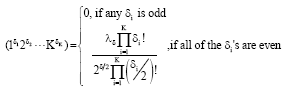 | (11) |
where, γδ is a quantity that depends on d, δ and N(Box and Hunter, 1957). According to Myers (1991), a second-order design with moments, which have the following conditions:
| • | All moments that have at least one δi to be odd are zero |
| • | Pure fourth moments, which is equal to |
| (12) |
is rotatable. Notice from the portion of a typical design matrix, X for general CCD containing the second-order terms that:
| (13) |
and
| (14) |
Of the two conditions given, which must be met in order that a second-order design is rotatable, the first is automatically met by mere inspection of X for the CCD (Myers, 1991). Thus, it only remains to find the value of α for which the second condition holds. Using Eq. 12-14 accordingly, we obtain:
| (15) |
Now for the information matrix in Eq. 7:
where, q = 2K n1 and p = 2K n1+2n2α4
Rotatably-restricted CCD: A CCD is rotatably-restricted if and only if 2K n1+2α4n2 = 3(2Kn1).
CUBE REPLICATIONS VERSUS STAR REPLICATIONS IN RESTRICTED CCD
For the sake of the comparison, denote the replicated cubes plus one star variation of restricted CCD by ξ. Also, denote the corresponding information matrix for this variation by M(ξ). Similarly, let η denote the one cube plus replicated stars variation of restricted CCD while M (η) denotes its information matrix. The criterion for comparison employed in this papers is the D-optimal design criteria, which is defined thus: given any two designs, ξ and η, with information matrices, M(ξ) and M(η), respectively, then ξ is preferred to η if the difference, M(ξ)-M(η) is positive definite, that is:
| (16) |
where, φ is the D-optimality criterion function which maximizes the determinant of the information matrix; for instance (Pazman, 1986; Fedorov, 1972; Onukogu, 1997):
| (17) |
The first restriction to be illustrated here is that for which the design is orthogonal. Recall that for orthogonality to be ensured in the CCD, the condition q = 0 must be satisfied, which implies that:
Hence,
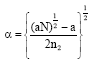 |
is the value that always gives an orthogonal CCD, where a = 2Kn1. Consequently, the information matrix in Eq. 7
becomes m0 = ![]() = diagonal (M1-IK, M2I1, p0IK) for: orthogonally-restricted CCD, where, p0 = 2n2α4. Putting
= diagonal (M1-IK, M2I1, p0IK) for: orthogonally-restricted CCD, where, p0 = 2n2α4. Putting
 |
in M1 and p0, we obtain:
and
Obviously, the eigenvalues of M0 are its diagonal elements. Hence, the ordered eigenvalues of M0 are:
where:
and ![]() each has K multiplicities in the above ordering while α has:
each has K multiplicities in the above ordering while α has:
multiplicities in the same ordering. We then have for the orthogonally-restricted CCD that the determinant of the information matrix is given by:
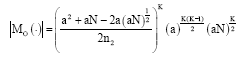 | (18) |
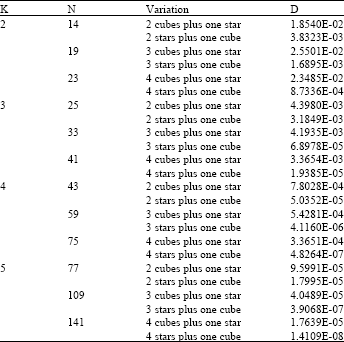
| Table 1: | Comparison of D-optimality values of the orthogonally-Restricted variations for Selected N-point CCD |
 | |
| Table 2: | Comparison of D-optimality Values of the Rotatably-Restricted Variations for Selected N-point CCD |
 | |
Therefore, its D-optimality value becomes:
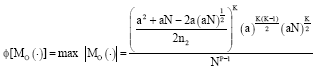 | (19) |
Using Eq. 19, the numerical values of φ[Mo(η)] and φ[Mo(ξ)] for each variation of orthogonally-restricted CCD given in Table 1 is obtained.
Another interesting and important restriction in this article is that of readability. A design is rotatable when the variance of the estimated response is a function of only the distance from the center of the design and not on the direction. Recall a CCD is rotatably-restricted if and only if 2K n1+2α4n2 = 3(2Kn1). Therefore:
always gives a rotatable CCD. Putting
in M1 and M3 of (7), we obtain M1a+2(αn2)1/2 and M3 = 2alK+aJK. Thus, the information matrix, MR for the rotatable CCD could be written as ![]() . It can easily be seen that the eigenvalues of MR has a regular pattern, hence, the ordered eigenvalues of this matrix are:
. It can easily be seen that the eigenvalues of MR has a regular pattern, hence, the ordered eigenvalues of this matrix are:
where, a has:
multiplicities, (a+2(an2)1/2) has K multiplicities, 2a has (K-1) multiplicities, and (K+2)a occurs only once in the ordering. We therefore have for the rotatably-restricted CCD that the determinant of the information matrix is given by:
| (20) |
Therefore, its D-optimality value becomes:
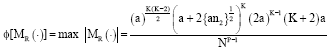 | (21) |
Using Eq. 21, the numerical values of φ[MR(ξ)] and φ[MR(η)] for each variation of rotatably-restricted CCD given in Table 2 are obtained.
RESULTS AND DISCUSSION
The following variations of the designs have been examined for illustration: one cube (n1 = 1) plus two replicated stars (n2 = 2); one cube (n1 = 1) plus three replicated stars (n2 = 3); one cube (n1 = 1) plus four replicated stars (n2 = 4); two replicated cubes (n1 = 2) plus one star (n2 = 1); three replicated cubes (n1 = 3) plus one star (n2 = 1) and four replicated cubes (n1 = 4) plus one star (n2 = 1). In Table 1 and 2, the results of the comparison are shown. We have obtained the numerical values of φ[MR(ξ)] and φ[MR(η)] for two, three, four and five factors. For each of these factors, three cases have been considered namely, Case one: two cubes plus one star versus one cube plus two stars: Case two: three cubes plus one star versus one cube plus three stars and Case three: four cubes plus one star versus one cube plus four stars. For each variation of N-point restricted CCD, at least two points are taken from the center in order to make up the required N points and also, to get a minimum of three degrees of freedom for pure error. Observe that the basis of variation in each case is the value of α which differs from each other for the two variations.
Table 1 and 2 summarize the comparison using the D-optimality values. We can note from the table that in all the three cases and for all the values of K considered, maximum D-optimality values were obtained when replicated cubes plus one star variation of both orthogonally-restricted CCD and rotatably-restricted CCD was used. That is, for the two conditions of restrictions, the strict inequality φ[MR(ξ)] ≥ φ[MR(ξ)] holds. A t-Test: Paired Two Sample for Means conducted afterwards between the D-optimality values of M(ξ) and M(η) revealed p-values of 0.02 and 0.04, respectively, for one-tailed and two-tailed tests for both orthogonal and rotatable restrictions of the CCD (indicating significant difference). Hence, this variation is preferred to one cube plus replicated stars variation of restricted CCD. We conjecture that this is true for any number of factors.
In general, the one cube plus replicated stars variation does not do well in this comparison.
CONCLUSION
The computational results in the tables show that the replicated cubes plus one star variation is better than the one cube plus replicated stars variation when any of the two restrictions considered in this work is imposed on a CCD. Since, in general, the D-optimality values of M(ξ) are significantly greater than those of M(η), we conclude that the replicated cubes plus one star variation is better than the one cube plus replicated stars variation in the sense of D-optimality criterion.
REFERENCES
- Box, G.E.P. and N.R. Draper, 1982. Measures of lack of fit for response surface designs and predictor variable transformations. Technometrics, 24: 1-8.
Direct Link - Box, G.E.P. and J.S. Hunter, 1957. Multifactor experimental designs for exploring response surfaces. Annal. Math. Stat., 28: 195-241.
Direct Link - Draper, N.R., 1982. Center points in second-order response surface designs. Technometrics, 24: 127-133.
Direct Link - Draper, N.R. and J.A. John, 1998. Theory and methods: Response-surface designs where levels of some factors are difficult to change. Aust. N. Z. J. Stat., 40: 487-495.
CrossRefDirect Link - Draper, N.R. and D.K.J. Lin, 1990. Small response surface designs. Technometrics, 32: 187-194.
Direct Link - Khuri, A.I., 1988. A measure of rotatability for response-surface designs. Technometrics, 30: 95-104.
CrossRefDirect Link - Montgomery, D.C., 1991. Design and Analysis of Experiments. 3rd Edn., John Wiley & Sons Inc., New York, Pages: 500.
Direct Link - Nalimov, V.V., T.I. Golikova and N.G. Mikeshina, 1970. On practical use of the concept of D-optimality. Technometrics, 12: 799-812.
Direct Link








