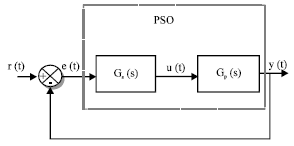
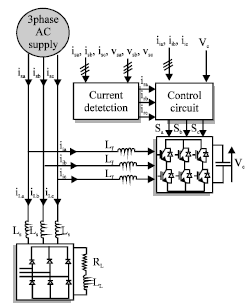
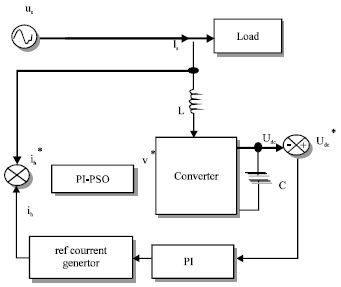
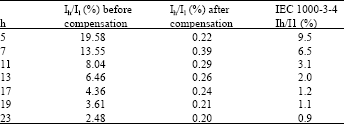
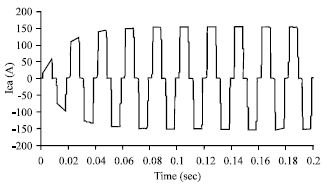
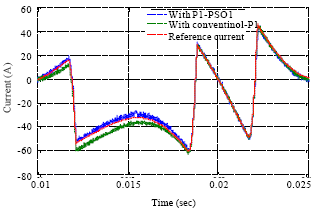
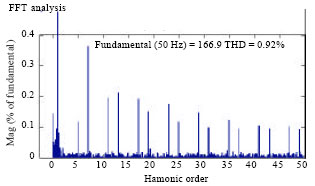
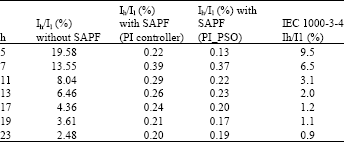
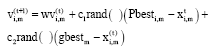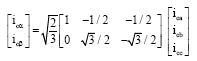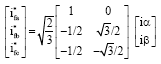Research Article
Power Quality Enhancement using Shunt Active Power Filter Based on Particle Swarm Optimization
Faculty of Electrical Engineering, Bechar University, BP. 417, Bechar 08000, Algeria
Chellali Benachaiba
Faculty of Electrical Engineering, Bechar University, BP. 417, Bechar 08000, Algeria