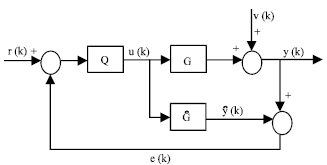
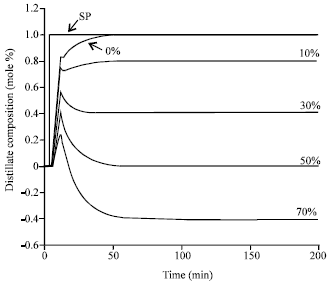
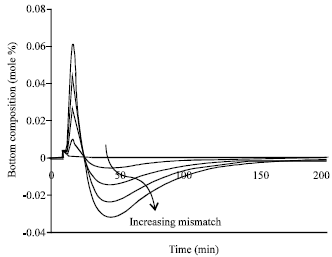
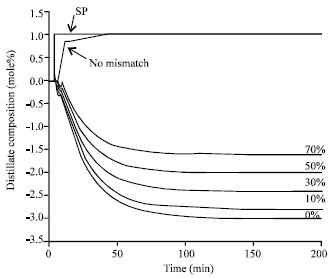
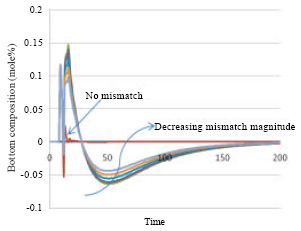
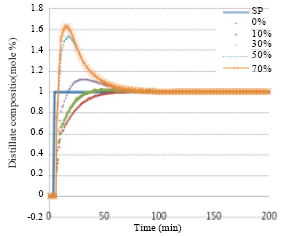
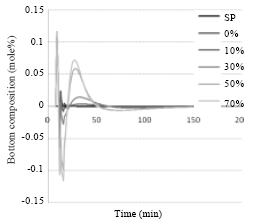
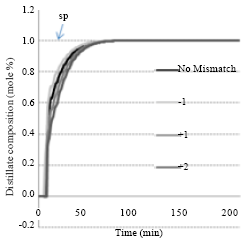
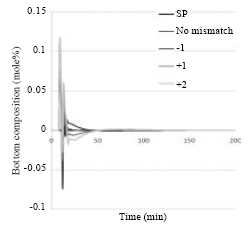
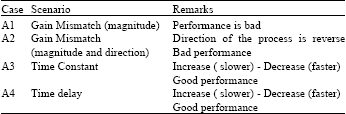
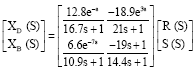Research Article
Effect of Model-plant Mismatch on MPC Controller Performance
Department of Chemical Engineering, Universiti Teknologi, PETRONAS, 31750, Tronoh, Malaysia
N. Yusoff
Department of Chemical Engineering, Universiti Teknologi, PETRONAS, 31750, Tronoh, Malaysia