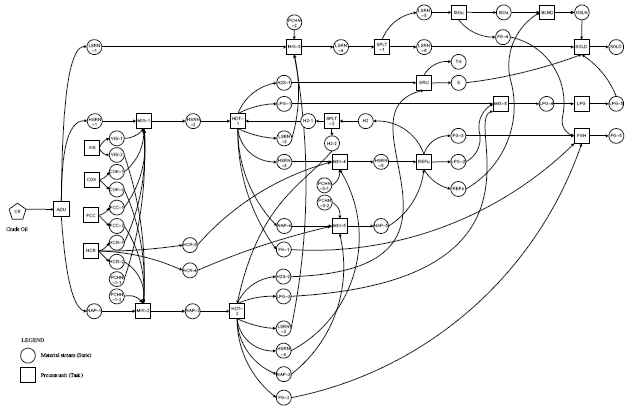
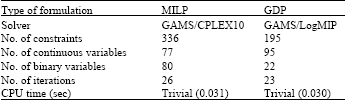
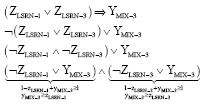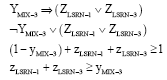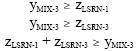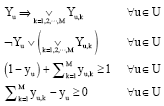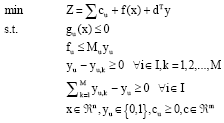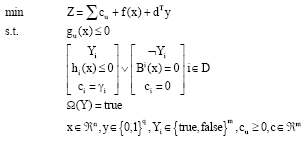Research Article
Optimal Design of Petroleum Refinery Topology using a Discrete Optimization Approach with Logical Constraints
Centre for Process Systems Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, United Kingdom
Xiao Qi Yeoh
Department of Reservoir Engineering, Reservoir Studies, Petroleum Engineering Division, PETRONAS Carigali Sdn Bhd., Level 17, Tower 2, Kuala Lumpur City Centre, 50088 Kuala Lumpur, Malaysia
Nilay Shah
Centre for Process Systems Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, United Kingdom