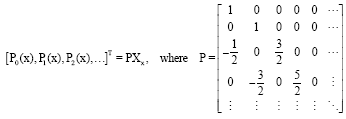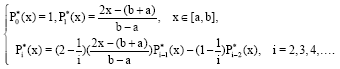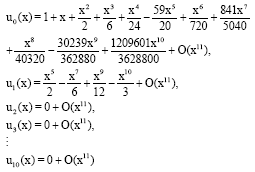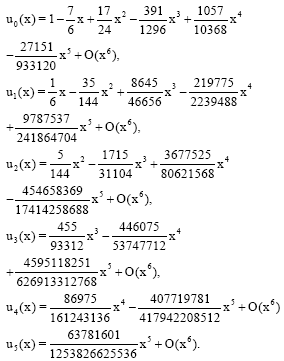Research Article
A Low-cost Numerical Algorithm for the Solution of Nonlinear Delay Boundary Integral Equations
Department of Mathematics, Islamic Azad University, Shahrekord Branch, P.O. Box 166, Shahrekord, Iran
S. Heidari
Department of Mathematics, Islamic Azad University, Shahrekord Branch, P.O. Box 166, Shahrekord, Iran
M. Avaji
Department of Mathematics, Islamic Azad University, Shahrekord Branch, P.O. Box 166, Shahrekord, Iran