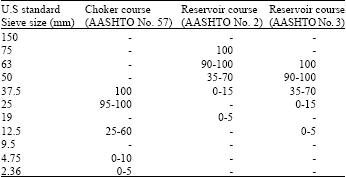
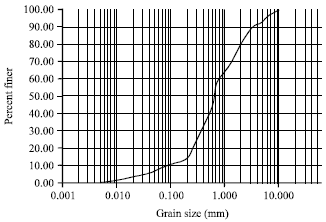
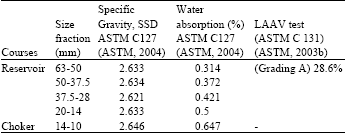
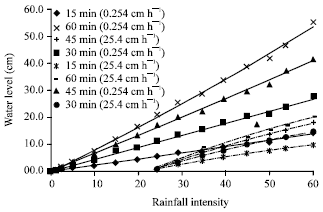
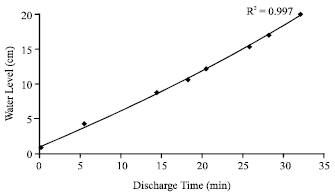
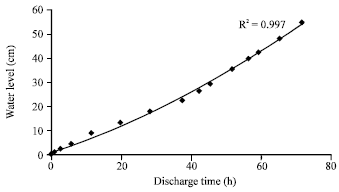
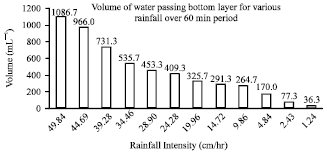
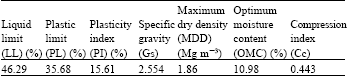Research Article
Laboratory Assessment of Water Flow Simulator for Porous Parking Lots Reservoir and Soil Layers
School of Civil Engineering, Engineering Campus, Universiti Sains Malaysia, 14300 Nibong, Tebal, Pulau Pinang, Malaysia
Zul Fahmi Mohamed Jaafar
School of Civil Engineering, Engineering Campus, Universiti Sains Malaysia, 14300 Nibong, Tebal, Pulau Pinang, Malaysia
Fauziah Ahmad
School of Civil Engineering, Engineering Campus, Universiti Sains Malaysia, 14300 Nibong, Tebal, Pulau Pinang, Malaysia