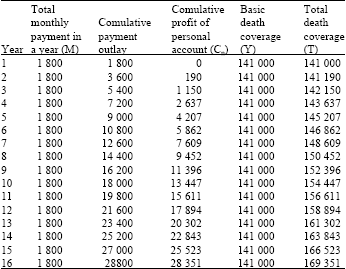
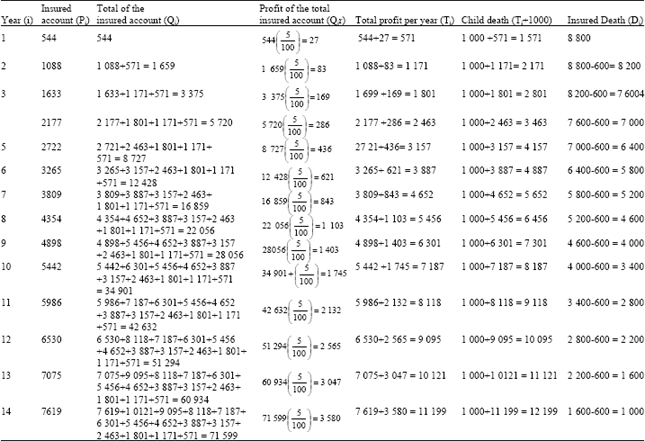
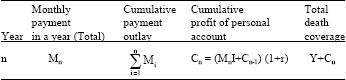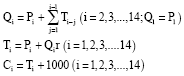Research Article
Mathematical Modelling in Family Takaful
Graduate School, Universiti Malaysia Terengganu, Malaysia
Ismail Bin Mohd
Department of Mathematics, Faculty Science and Technology, Universiti Malaysia Terengganu, 21030 K, Terengganu, Malaysia
Mustafa Bin Mamat
Department of Mathematics, Faculty Science and Technology, Universiti Malaysia Terengganu, 21030 K, Terengganu, Malaysia
Wan Muhamad Amir W. Ahmad
Department of Mathematics, Faculty Science and Technology, Universiti Malaysia Terengganu, 21030 K, Terengganu, Malaysia