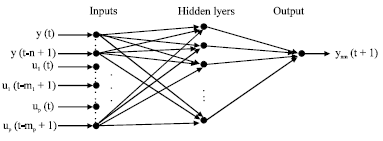
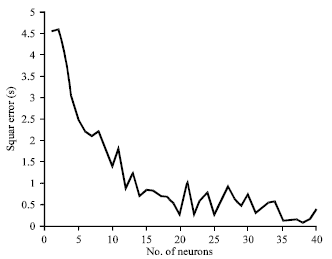
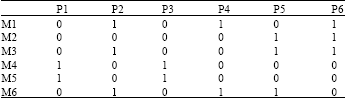
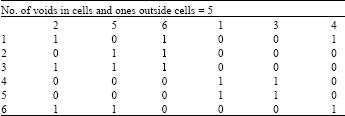
Research Article
Optimal Computerized Model for Designing Cellular Manufacturing Systems using Neural Network
Department of Industrial Engineering, The Hashemite University, P.O. Box 150459, Zarqa 13115, Jordan
Sahar Idwan
Department of Computer Science and Applications, The Hashemite University, P.O. Box 150459, Zarqa 13115, Jordan
Moh`d Sami Ashhab
Department of Mechanical Engineering, The Hashemite University, P.O. Box 150459, Zarqa 13115, Jordan
Murad Samhouri
Department of Industrial Engineering, The Hashemite University, P.O. Box 150459, Zarqa 13115, Jordan
Izzeddin A. Matar
Department of Software Engineering, Faculty of Information Technology, Petra University, Queen Alia International Road, P.O. Box 961343, Amman 11196, Jordan