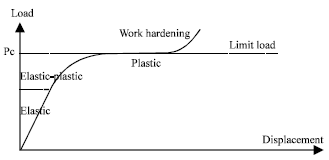
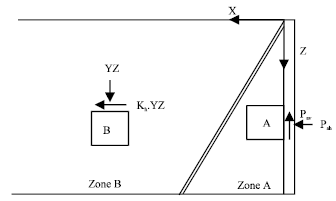
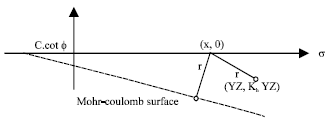
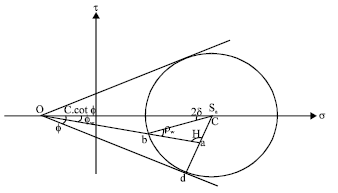
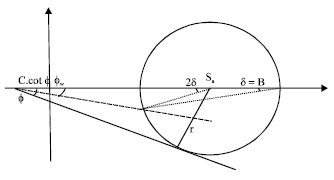
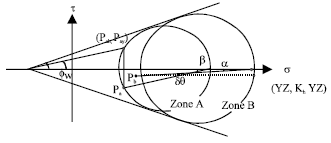
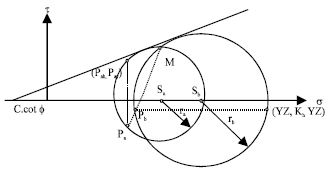
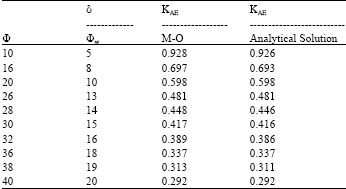
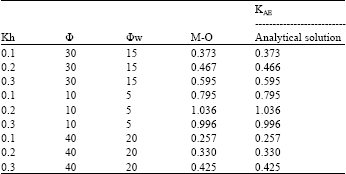
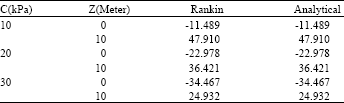
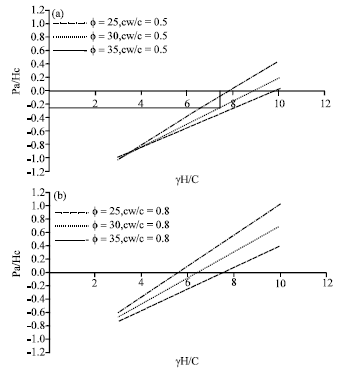
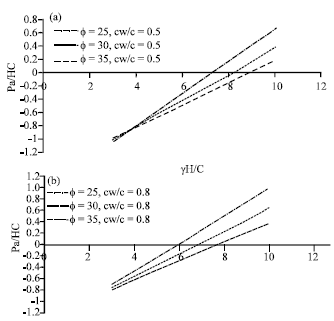
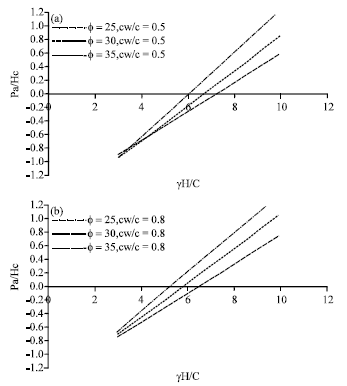
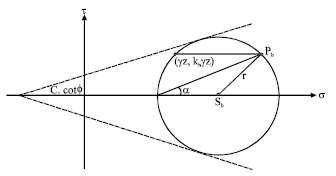
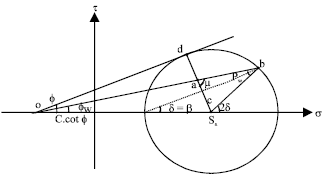
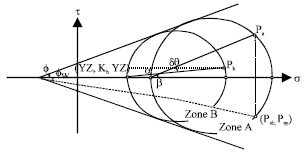
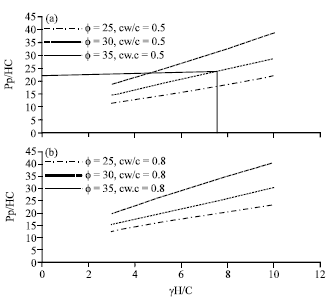
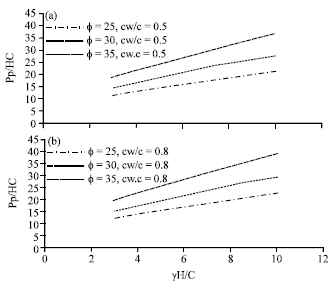
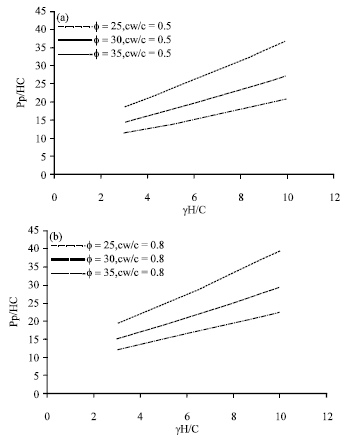
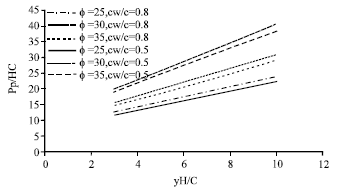
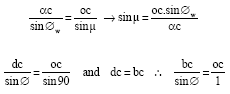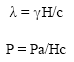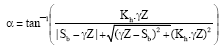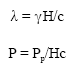Research Article
Non-Dimensional Seismic Charts of Active and Passive Forces in Retaining Walls using Stress Fields
Department of Civil, Marvdasht Branch, Islamic Azad University, Marvdasht, Fars, Islamic Republic of Iran
Farajolah Askari
Iran International Earthquake Engineering Institute, Tehran, Islamic Republic of Iran