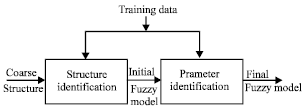
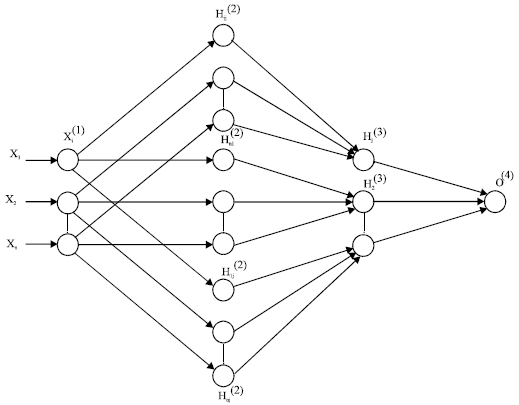
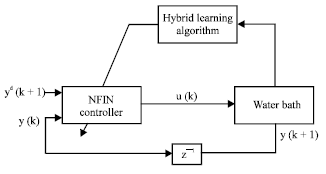
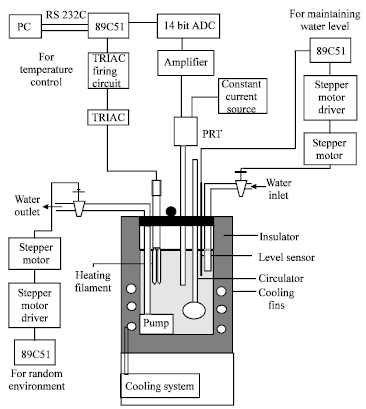
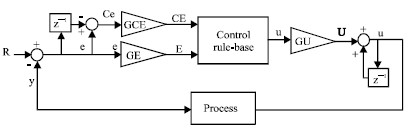
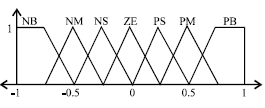
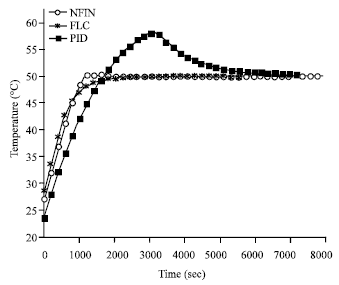
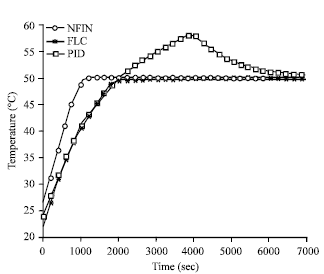
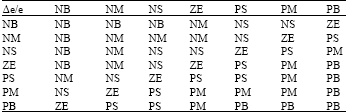
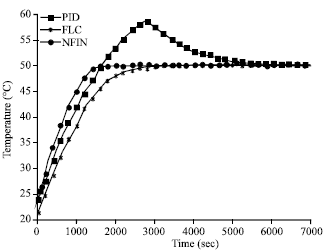
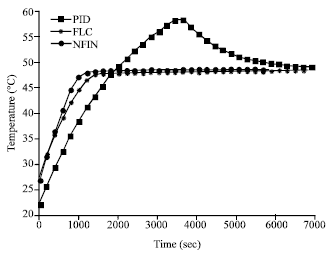
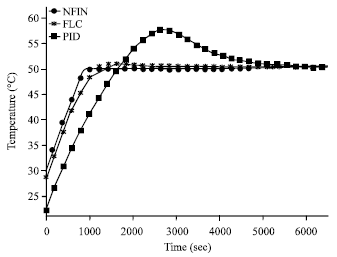
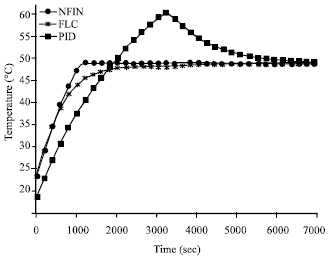
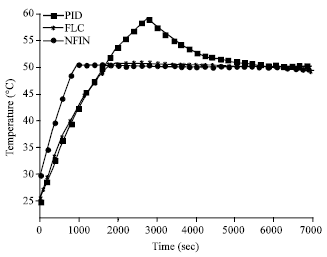
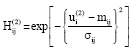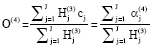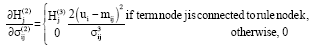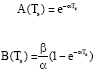Research Article
Optimal Design of Neural Fuzzy Inference Network for Temperature Controller
Department of Electronics, University of Delhi South Campus, New Delhi 110 021, India
Udaibir Singh
Department of Electronics, Acharya Narendra Dev College, University of Delhi, Govindpuri, Kalkaji, New Delhi 110019, India
T. K. Saxena
National Physical Laboratory, Dr. K.S. Krishnan Road, New Delhi-110 012, India
Avinashi Kapoor
Department of Electronics, University of Delhi South Campus, New Delhi 110 021, India