Research Article
Statistical Analysis of the Relationship Between Wind Speed, Pressure and Temperature
Department of Mathematics and Statistics, University of South Florida, Tampa, Florida 33620, United States of America
In the present study, a new method has been introduced for the estimation of parameters in both univariate and multivariate analysis using real world data to continue analyzing the relationship between wind speed and pressure. Wind can be defined simply as air in motion, (Pidwirny and Slanina, 2010) and according to Newton's second law (Norbury and Roulstone 2002), assuming the mass of the wind is unchanged (constant density), the pressure gradient acceleration (the acceleration of the wind) is directly proportional to the difference in pressure. Hence, if we assume the mass and density of the air are constant, then wind speed is directly proportional to pressure, a ∝ ΔP and w ∝ P. This question was addressed using standard Regression Analysis by Wooten and Tsokos (2009a,b) in "A proposed new scale to identify the category of a Hurricane's status." In this study, five storms which had reached hurricane status category five according the Saffir-Simpson scale (Saffir, 1973; Simpson, 1974) were analysis to determine the relationship between wind speed and pressure and in other publications, (Wooten and Tsokos, 2008). To further test this relationship, the relations were re-analyzed using this new statistical method and then extended this to include non-response analysis together with interaction between wind speed and pressure. However, wind formation is a result of temperature difference; pressure and wind speed are co-dependent on temperature. According to the Ideal Gas Law, the interaction of pressure and volume are proportional to temperature, PV ∝ T and by Boltzmann's equation (Crummer, 2010), velocity-squared is proportional to temperature, w2 ∝ T. Therefore, to test for the affects of temperatures the analysis was further extended and the issue of volume has also been addressed (Powell and Reinhold, 2009).
It has been shown that the relationship between wind speed and pressure are co-dependent with temperature. It was first considered the relationship between wind speed and pressure within a storm and then considered more complex relationships between wind speed, pressure and temperature near the surface of the water. Having identified statistically the relationship in the subject data, it allows meteorologist to determine estimates of each variable as a function of the other variables, depending on the time of year and on the non-functional relationship obtained. Understanding the non-functional relationship between temperature, pressure and wind speeds is useful in understanding the dynamics that exist within a tropical storm.
DESCRIPTION OF DATA AND CONCEPT FOR COMPARISON
The two methods used in this study are standard multiple regression analysis for the statistical model
where
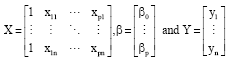 |
we have
| (1) |
and Wooten's augmented matrix for regression without a subject response, that is, non-response analysis for the statistical model:
defines the augmented matrix as:
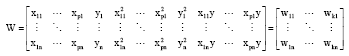 |
with parameters and unity:
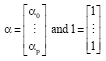 |
respectively; the parameters are the weights that balance the model to one and unity is a column vector of ones. Therefore we have
| (2) |
The data for the first part of the study are taken from website (http://weather.unisys.com/hurricane/index.php); wind speed and pressure readings for five hurricanes which reached hurricane status category five; namely, Isabel (2003), Ivan (2004), Katrina (2005), Rita (2005) and Wilma (2005). With readings every three hours, we have a sample of size 397. For the second part of the study, we will use hourly readings by buoy 42036 in the Gulf near Florida, (NBDC, 2005). With nearly 345 days of hourly readings, we have a sample of size 8277. There variables included in this second data set include pressure and wind speed in addition to temperatures (atmospheric, water and dew point) from which we will use Wooten's augmented matrix to determine the relationship that exist among the variables including interaction between the wind speed and pressure.
STANDARD ANALYSIS AND WOOTEN'S AUGMENTED MATRIX ESTIMATE
Using standard statistical methods, we were able to find the relationship between wind speed and pressure using the model relating pressure to wind speed and acceleration.
Then using standard statistical methods for multiple regression, we have the following data matrices:
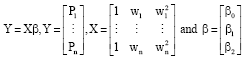 |
and we find the parameter estimates using Eq. 1; apply this statistical method to the first data set, the developed model is:
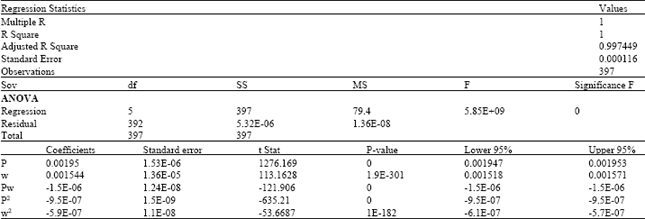
The parameter estimates are given in Table 1 including the analysis of variance and regression statistics. This model indicates that when there is no wind present, the atmospheric pressure is approximately 1012.96 millibars; standard atmospheric pressure is 1013.25 millibars. As shown in Table 1, an estimated 92% of the variance in the pressure is explained by wind speed in this regression model. With a standard error of 9.2, this model is useful in explaining the relationship between wind speed and pressure as shown in Fig. 1.
As proof on concept, we will estimate this same relationship using Wooten's augmented matrix and compare the results.
The alternative model is:and the augmented data matrices are given below:
 |
and parameter estimates the parameter estimates are given by Eq. 2; therefore, using this newly outlined method, we have the relationship among pressure and wind speed with second order in the wind speed only is found to be:
| Table 1: | Output summary for standard multiple regression, P = f (w) |
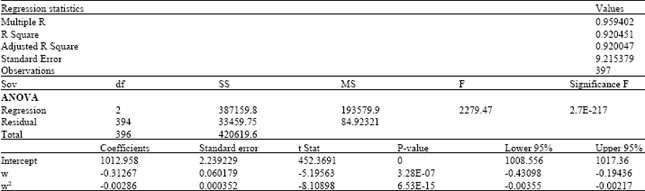 | |
| Table 2: | Output summary using wooten's augmented matrix, f (P) = 1 |
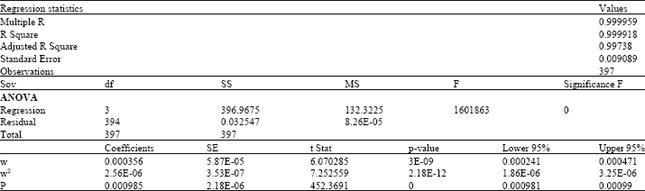 | |
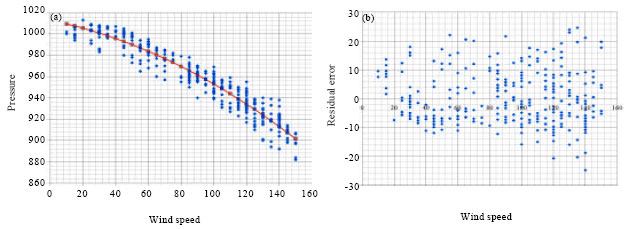 | |
| Fig. 1: | (a) Scatter plot of pressure versus wind speed including developed model and (b) residual plot |
The parameter estimates are given in Table 2 including the analysis of variance and regression statistics; with 99.99% of the points falling into this relationship, the approximate standard error (0.009089 in scale) of 9.23; this shows that these two statistical methods are comparable in terms of regressions to the surface (plane). Modeling done using standard multiple-regression can also be done using augmented matrices. This gives a scaled model in terms of pressure as a function of wind speed of ![]() as shown in Fig. 2.
as shown in Fig. 2.
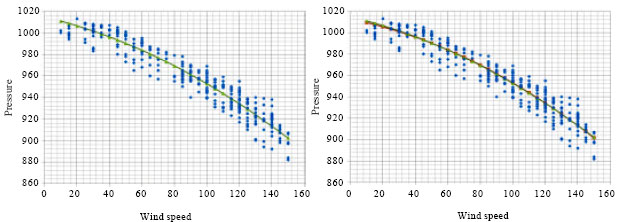 | |
| Fig. 2: | (a) Scatter plot of pressure versus wind speed including newly developed model and (b) a comparison of the two |
This comparison is further illustrated in the estimate of standard atmospheric pressure; using standard regression this was estimated to be 1012.96 and using Wooten's augmented matrix and model scaling, this estimate is 1014.9. The apparent differences are due to the fact that the data used to calibrate both models where recorded under hurricane conditions and therefore standard atmospheric pressure is extrapolated information.
NON-RESPONSE ANALYSIS
The above models are comparable, using Wooten's Augmented Matrix, the advantage to using augmented matrices over matrix equations is that we can extend this to include higher order terms in wind speed and pressure as well as interaction between the two terms and test the co-dependent relationship between the variables.
First we will test the relationship between wind speed and pressure assuming interaction and then with the full second order model.
First order interaction: Consider the augmented model including interaction without second order terms:
with data matrices given below:
 |
Using the developed non-response analysis, we have to be:
This gives a scaled model in terms of the smallest coefficient of
Where the parameter estimates are given in Table 3.
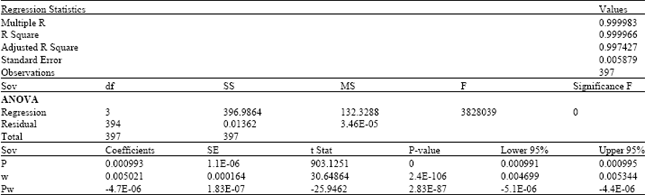
The parameter estimates are given in Table 3; with 99.997% of the points falling into this relationship, the approximate standard error 0.005879 which is less error than the previously developed model. Solving for pressure we have:
as shown in Fig. 3.
As indicated in Fig. 3, there are more points above the curve at the extremes and more points below the curve toward the center. However, there is a smaller standard error, this is an indication of higher order terms in at least one of the principle factors to explain the curvature seen in the residuals (Fig. 4).
Full second order model: Consider the augmented model:
with data matrices given below:
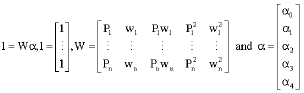 |
| Table 3: | Output summary for first order interaction, 1 = α0 P + α1w + α2 wP |
 | |
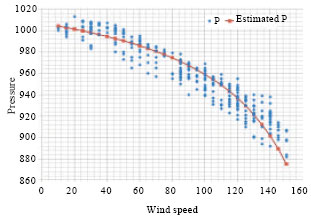 | |
| Fig. 3: | Scatter plot of pressure versus wind speed including developed model including interaction |
Using this non-response analysis, we have to be:
which gives a scaled model in terms of the smallest coefficient is:
| (3) |
Solving for pressure in terms of wind speed, we have
 |
The parameter estimates are given in Table 4; with 100% of the points falling into this relationship, the approximate standard error 0.000116 which is less error than the standard error found in the two previously developed models.
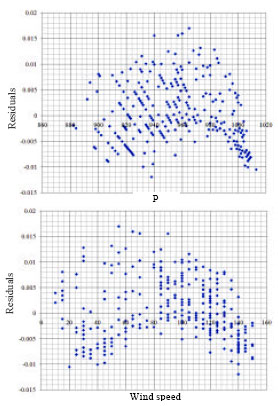 | |
| Fig. 4 (a-b): | Residual plot of (a) pressure and (b) wind speed |
Solving for pressure we have:
| (4) |
with parameter estimates given in Table 4 and the model shown graphically in Fig. 5,
where:
The apparent reason for the two solutions is that pressures relationship to wind speed is indirectly related by temperature and volume and therefore, the pressure would be different before, during and after a storm.
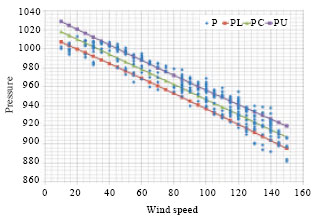 | |
| Fig. 5: | Scatter plot of pressure versus wind speed including developed model including higher order terms and interaction |
This is seen in the estimates when we let:
as shown in Fig. 6, this rule applies more so for the early stages of the storm and later states of the storm when wind speeds are low; however, when the wind speeds are greater than 80 knots, the pressures appear mainly between these two extremes.
This is an indication that there are lurking variables, either volume (not measured) or temperatures (not provided in this data set) are related to pressure and wind speed. This breakdown is consistent with the Wooten and Tsokos (2009b) scale, that around 80 knots there is a shift in pressure differentials and the start of hurricane category 2 in this newly defined scale.
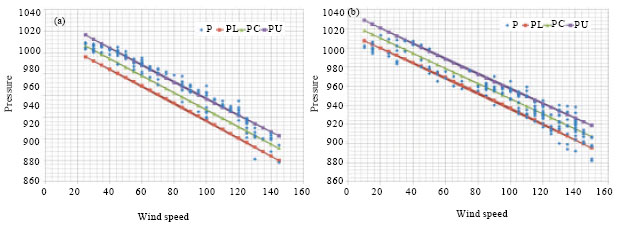 | |
| Fig. 6 (a-b): | Scatter plot of pressure versus wind speed (a) before the storm and (b) after the storm |
| Table 4: | Output summary for full second order model, 1 = α0 P + α1w + α2wP + α3P2 + α4w2 |
 | |
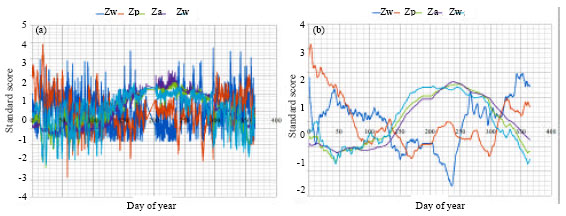 | |
| Fig. 7 (a-b): | Standard scores for wind speed, pressure, temperatures (atmospheric, water and dew point) for (a) the original data and (b) for the 28-day moving average |
In the Saffir-Simpson scale, this shift occurs at 85 knots.
COMPARISON TO BUOY DATA WHEN NO STORMS ARE PRESENT
Next the relationship has been tested between wind speed and pressure first assuming interaction alone and then with the full second order model using data measured every hour near the surface of the ocean as opposed within a storm with hurricane force winds. As these values vary from hour to hour and have daily and yearly patterns, Fig. 7a, the 28-day moving average for wind speed, pressure and temperatures (atmospheric, water and dew point)has been considered, Fig. 7b.
To compare these measures near the surface to those measured within a hurricane; consider the non-response model given in Eq. (3). Using this non-response analysis and the raw data, we have to be:
which gives a scaled model is:
Solving for pressure in terms of wind speed, we have
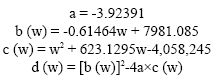 |
Hence, solving for pressure as it has been done in the previous analysis, Eq. (4), the developed model estimated the central tendency linearly using Pc with volatility as indicated in the upper and lower pressure estimates. However, as the wind speed increase, this estimate has increase variance.
Figure 8 indicates that there is more to the relationship between pressure and wind speed near the surface of the water in the Gulf of Mexico. This is seen in that the estimates for pressure are only accurate during the summer months when temperatures are higher. However, in the winter months, the developed model does not accurate estimate the observed pressure. This is due to the affects of temperature. By the ideal gas law, pressure and volume are directly related to temperature, but under the assumption that pressure is constant, by Charles Law (Pidwirny, 2006), here the ratio of volume to temperature is constant. Therefore, during the summer months when pressures appear to be constant, temperature should explain the interaction between pressure and volumes. To compare the behavior of each of the various temperatures and related volumes by scaling the data as follows: given a variable x, define the scaled value of the data, y, to be:
Among the variables given, pressure appears to be most constant; in addition, the behaviors of the three temperature readings are very similar. This is seen in Fig. 9, while the dew point is higher than the atmospheric temperature and water temperature is lower than atmospheric temperature, during hurricane season, they rise and fall comparatively. When compared to the other variables, temperature appears to relate inversely; when temperatures rise, pressure and wind speed compensate for the moving volumes of air. This direct relationship between temperatures and volumes (holding pressure constant in the Ideal Gas Law) will allow us to treat volume as a constant as V ∝ T.
 | |
| Fig. 8(a-b): | (a) Line graph of estimated pressures over time (day of year) and (b) scatter plot of estimated pressure versus wind speed |
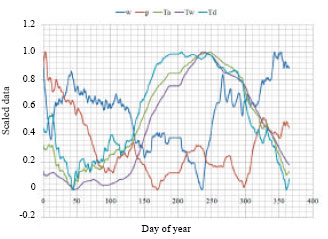 | |
| Fig. 9: | Scaled data: wind speed, pressure and temperatures (atmospheric, water and dew point) |
To address the constant nature of the remaining variables starting with pressure, consider the non-response model:
with data matrices are given below:
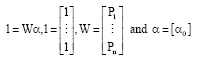 |
and parameter estimate:
This measure is also an indication of the constant nature of the variable itself. Consider the sums of square error for the variable P:
then the sums of squares are a measure of the mean and the sum of square errors:
Hence, internal to the variable, the coefficient of determination is the percent of total sums of squares explained by the mean and is given by:
As ![]() and therefore P is approximately a constant and as
and therefore P is approximately a constant and as ![]() and therefore P is extremely variant.
and therefore P is extremely variant.
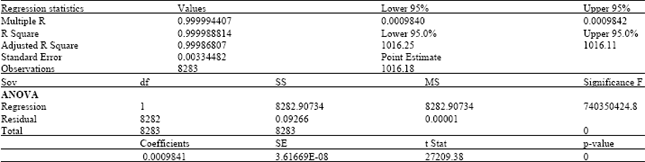
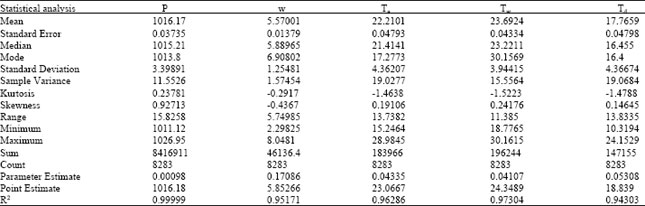
Table 5 gives the analysis of the constant nature of the variable pressure. In this data set, the pressure is relatively constant with R2 = 0.99999. The estimate of the mean reciprocal is 0.0009841, which gives a point estimate for standard atmospheric pressure of 1016.18.
Compare the variability of the five given variables, Table 6; the most variant measure is the dew point with R2 = 0.94303, followed by wind speed with R2 = 0.95171, atmospheric temperature with R2 = 0.96286, water temperature with R2 = 0.97304 and lease variant is pressure with R2 = 0.99999. The point estimates using the standard sample mean are lower compared to the point estimates found using Wooten's Augmented Matrix as this alternative method uses the variance in the data to estimate the population mean.
| Table 5: | Summary output for non-response analysis of means for pressure, P |
 | |
| Table 6: | Summary Output for comparison of non-response analysis by variable: Pressure, Wind Speed, Temperatures (Atmospheric, Water, Dew Point) |
 | |
| Table 7: | Correlation Matrix between variables: Pressure, Wind Speed, Temperatures (Atmospheric, Water, Dew Point) |
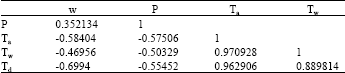 | |
To address the similar behaviors seen in the three different temperature readings, shown in the correlation matrix in Table 7, these temperatures are highly correlated with a minimum correlation coefficient of 0.8898 between dew point and water temperature; water temperature and dew point are both highly atmospheric temperature. Therefore, as dew point is a measure of relative humidity (volume) and follows a similar pattern to both atmospheric and water temperature, we will use dew point as the temperature reading.
Consider the non-response model using dew point as the measure of temperature:
Using non-response analysis, the developed model is:
|
where, solving for pressure we have:
 |
with parameter estimates given in the developed model; shown graphically in Fig. 10, where similar to Eq. 4, we have:
Similarly, we can rotate our focus by either solving in terms of temperature or wind speed. First solving for temperature, we have:
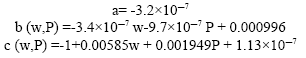 |
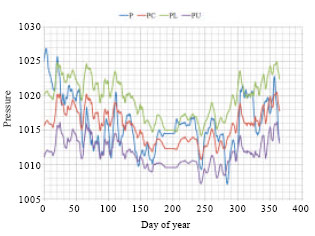 | |
| Fig. 10: | Estimated pressure along with observed pressure using 7-day moving averages over time (day of year) |
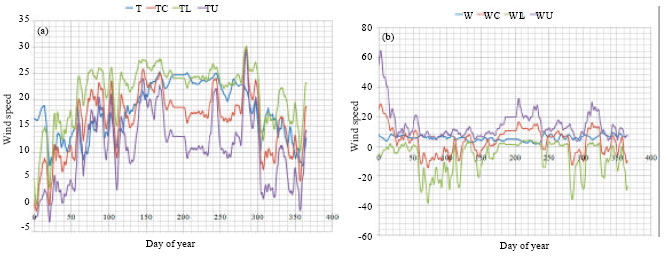 | |
| Fig. 11: | (a) Estimated temperatures with the observed temperature (dew point) using 7-day averages over time (day of year) and (b) estimated wind speed along with observed wind speed using 7-day moving averages over time (day of year) |
and as shown in Fig. 11a, the temperatures generally follow either upper or lower solution and varying in between the Eq:
Solving in terms of wind speed, we have:
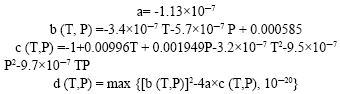 |
and therefore, as show in Fig. 11b, wind speeds following one of the two solutions:
As with pressure, pressure and wind speed find balance in one of two solutions to the given equation. During the winter days, the true value of the wind speed appear to follow the upper solution, however, in the summer days (when temperatures are higher), the wind speeds appear to follow the lower solution. This reverses in the estimates of temperature, Fig. 11b; in the summer, the data follows the upper solution and in the winter is best estimated by the lower solution or approximately the central solution. In general, the solution with minimum wind speed is optimal; that is, the estimated wind is always that with minimum velocity, v = |w|.
USEFULNESS OF NON-RESPONSE ANALYSIS
The usefulness of non-response analysis is that it provides alternative parameter estimates for standard multiple regressions and allows the analysis to go beyond functional analysis of dependent and independent variables to that of co-dependent relationship. This additional point of view offers insight into the subject phenomenon and allows us to test assumptions without assigning the title of response variable and explanatory variable but rather related variables.
We have shown that temperature is related to wind speed and pressure when no storms are present; therefore, observing temperatures is necessary to understand when low pressures result in higher wind speeds like those found within a hurricane.
Using statistical regression and non-response analysis, pressure can for the most part be explained by wind speed. However, according to simple correlation analysis, wind speed near the surface is most highly correlated with the temperature, of which, dew point is related to the relative humidity and the density of the air. Pressure is also highly correlated with atmospheric temperature. In fact, the pressure appears to be co-dependent with wind speed and temperature. There are two solutions for pressure depending on the temperature and wind speed. Similarly, there are two solutions for wind speed depending on pressure and temperature. In pressure, the solution appear to depend on the temperature, such as before and after a storm has reached maximum sustained winds; however, when solving for wind speed, the solution is that which minimizes the velocity.
I would like to express my appreciation to Dr. Chris P. Tsokos, my mentor; and Kavita Kulkarni and Wanda Works for their encouragement and review.