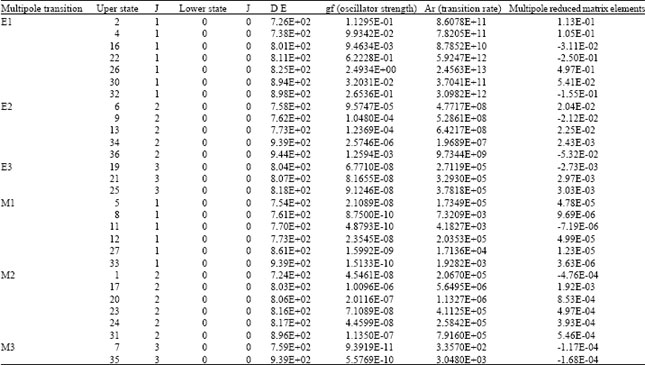
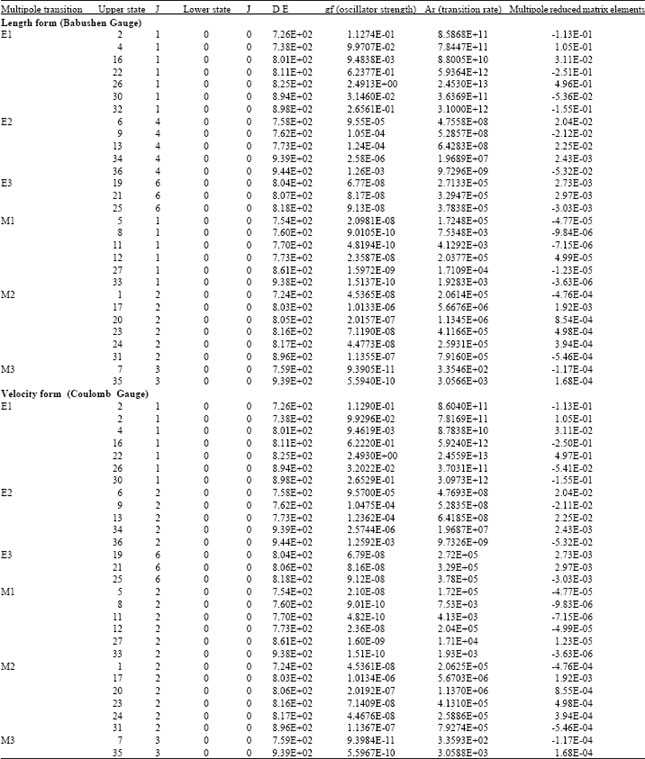
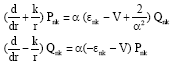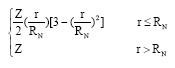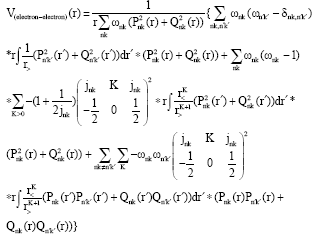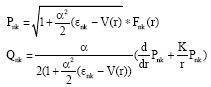Research Article
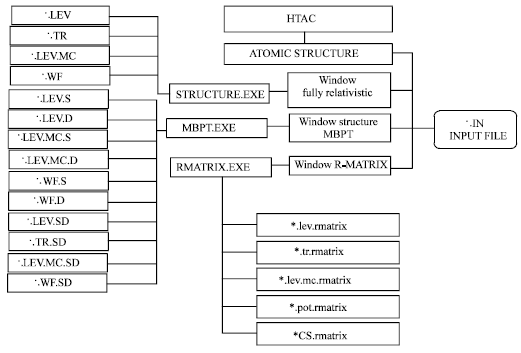
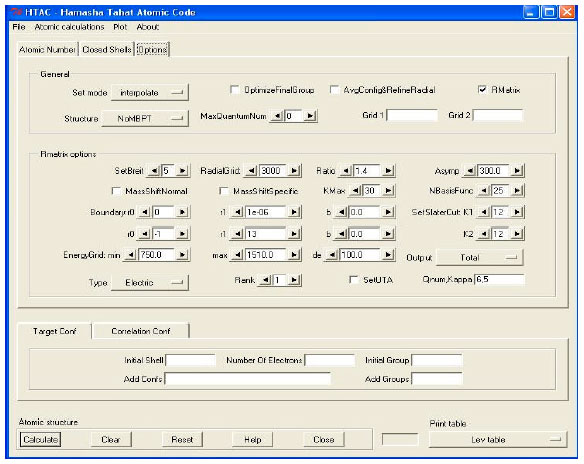
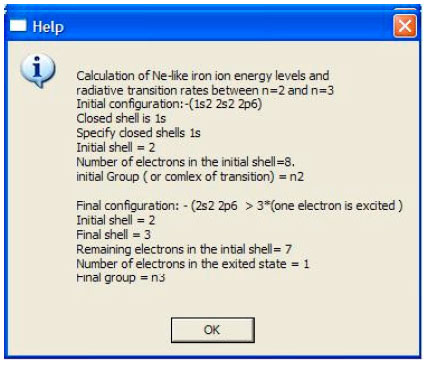
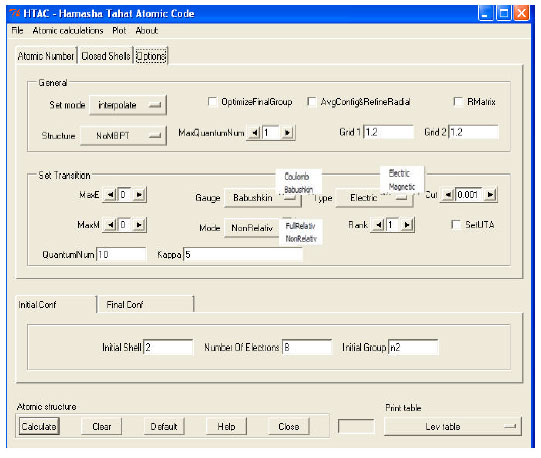
Developing a New Atomic Physics Computer Program (HTAC) to Perform Atomic Structure and Transition Rate Calculations in Three Advanced Methods
Department of Physics, Faculty of Science, Hashemite University, P.O. Box (150459), Zarqa 13115, Jordan
Mahmoud Abu Allaban
Department of Physics, Faculty of Science, Hashemite University, P.O. Box (150459), Zarqa 13115, Jordan
Amani Tahat
Faculty of Natural Resources, Hashemite University, P.O. Box 150459, Zarqa 13115, Jordan