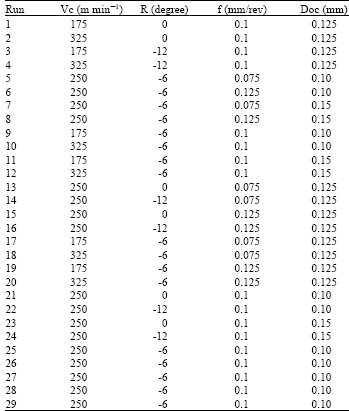
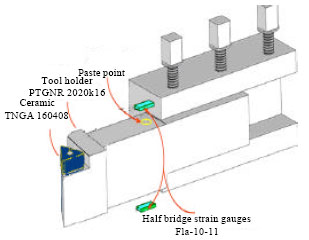
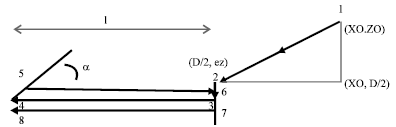
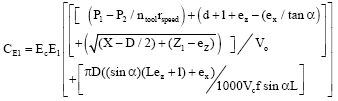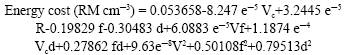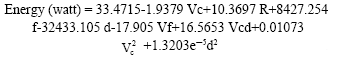Research Article
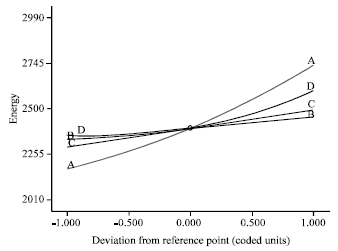
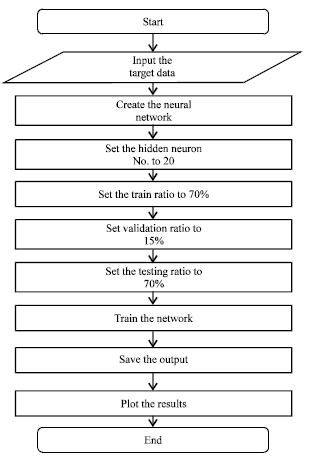
Energy Cost Modeling for High Speed Hard Turning
Department of Manufacturing and Materials Engineering, Faculty of Engineering, International Islamic University Malaysia, 53100 Gombak, Kuala Lumpur, Malaysia
Erry Yulian T Adesta
Department of Manufacturing and Materials Engineering, Faculty of Engineering, International Islamic University Malaysia, 53100 Gombak, Kuala Lumpur, Malaysia
Afifah Mohd Ali
Department of Manufacturing and Materials Engineering, Faculty of Engineering, International Islamic University Malaysia, 53100 Gombak, Kuala Lumpur, Malaysia
Delvis Agusman
Department of Mechanical Engineering, Faculty of Engineering, University Tarumanagara, Jakarta, Indonesia
Mohammad Yuhan Suprianto
Department of Manufacturing and Materials Engineering, Faculty of Engineering, International Islamic University Malaysia, 53100 Gombak, Kuala Lumpur, Malaysia