ABSTRACT
We review the non-commutative geometry in the second-class constraints. We show the non-commutativity in the space-time coordinates based on quantum field theory and matrix theory compactifications has correspondence to the non-commutativity in the space-time coordinates based on the second-class constraints.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2011.199.200
URL: https://scialert.net/abstract/?doi=jas.2011.199.200
INTRODUCTION
Even in the early days of quantum mechanics and quantum field theory, continuous space-time and Lorentz symmetry was considered inappropriate to describe the small-scale structure of the universe. It was also argued that one should introduce a fundamental length scale limiting the precision of position measurements. Snyder was the first to formulate these ideas mathematically. He introduced non-commutative coordinates. Therefore, a position uncertainty arises naturally. The success of the renormalization program made people forget about these ideas for some time. However, when the quantization of gravity was considered thoroughly, it became clear that the usual concepts of space-time are inadequate and the space-time has to be quantized or non-commutative (Connes, 1994; Witten, 1996). As a result, there is a deep conceptual difference between quantum field theory and gravity: In the former, space and time are considered as parameters, in the latter as dynamical entities. To resolve the problem, quantum mechanics in non-commutative space (NCQM) was developed. If NCQM is a realistic physics, all the low energy quantum phenomena should be reformulated in it. In literature, NCQM have been studied in detail (Chaichian et al., 2001; Gamboa et al., 2001; Hatzinikitas and Smyrnakis, 2002; Ho and Kao, 2002; Nair and Polychronakos, 2001; Zhang, 2004; Farmany, 2005, 2010; Farmany et al., 2009a-c). In this letter, we focus on the non-commutative geometry in the second-class constraints.
NON-COMMUTATIVE GEOMETRY
According to Dirac's procedure for dealing with constrained systems, Dirac brackets must replace those constraints, which do not commute with all other (the second-class constraints), must be solved explicitly or their Poisson brackets, but the first and second-class constraints are mixed up. Convincing ways have been found to disentangle them in a covariant manner by Ghosh (1994).
Let us begin with the Lagrangian of an anyon in the background gravity:
| (1) |
Where:
and gμv is the space-time metric.
In the non-Abelian gauge interactions the canonical momenta are:
| (2) |
| (3) |
In our framework, from the four primary constraints we can write:
| (4) |
| (5) |
| (6) |
| (7) |
where, λ = M/J Using analytical methods, from four primary constraints we can construct further constraint set (Chou et al., 1993). We focus on the second-class constraint set (Vμ, χμ) (Dirac, 1964) The Poisson bracket matrix of the constraint set (Vμ, χμ) is:
| (8) |
In addition, the inverse Poisson bracket is defined by:
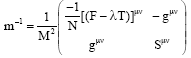 | (9) |
Where:
and Tμv is the torsion term and N, M and F are three dimensional matrixes.
According to Dirac's procedure for dealing with constrained systems, those constraints that do not commute with all other ones the second-class constraint must be solved explicitly or their Poisson brackets must be replaced by Dirac brackets. Let xμ and xv be the coordinates. Using Eq. 8 we can write the generic Dirac bracket for coordinates as:
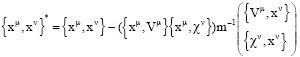 | (10) |
Equation 10 can be simplified to:
| (11) |
where, Sμv is a matrix and ![]() have dimension of x2. Equation 11 shows the generic non-commutativity in the geometry of the space-time.
have dimension of x2. Equation 11 shows the generic non-commutativity in the geometry of the space-time.
CONCLUSION
The non-commutative geometry in the second-class constraints is studied. It is shown that the non- commutativity in the space-time coordinates based on quantum field theory and matrix theory compactifications is correspondence to the non-commutativity in the space-time coordinates based on the second-class constraints.
REFERENCES
- Chaichian, M., M.M. Sheikh-Jabbari and A. Tureanu, 2001. Hydrogen atom spectrum and the lamb shift in noncommutative QED. Phys. Rev. Lett., 86: 2716-2719.
PubMed - Chou, C., V.P. Nair and A.P. Polychronakos, 1993. On the electromagnetic interactions of anyons. Phys. Lett. B, 304: 105-110.
CrossRef - Farmany, A., 2005. Spinning particles and non-commutative geometry. Phys. Scripta, 72: 353-353.
CrossRef - Farmany, A., R. Lotfikar, S. Abbasi, A. Naghipour and A. Farmany, 2009. Non-commutative geometry and matrix quantum mechanics. Chaos Solitons Fractals, 42: 62-64.
CrossRefDirect Link - Farmany, A., S. Abbasi, A. Naghipour, A. Nuri and N. Rahimi, 2009. Classical black-brane and non-commutative geometry. Chaos Solitons Fractals, 41: 1518-1519.
CrossRefDirect Link - Farmany, A., S. Abbasi, M.T. Darvishi, F. Khani and A. Naghipour, 2009. Minimal length uncertainty and generalized non-commutative geometry. Chaos Solitons Fractals, 42: 2833-2835.
CrossRef - Farmany, A., 2010. A proposal for spectral line profile of hydrogen atom spectrum in the sub-nano-meter space time. J. Applied Sci., 10: 784-785.
CrossRef - Gamboa, J., M. Loewe and J.C. Rojas, 2001. Noncommutative quantum mechanics. Phys. Rev. D, 64: 067901-067903.
CrossRef - Ghosh, S., 1994. Spinning particles in 2 + 1 dimensions. Phys. Lett. B, 338: 235-240.
CrossRefDirect Link - Hatzinikitas, A. and I. Smyrnakis, 2002. The noncommutative harmonic oscillator in more than one dimension. J. Math Phys., 43: 113-125.
CrossRef - Ho, P.M. and H.C. Kao, 2002. Noncommutative quantum mechanics from noncommutative quantum field theory. Phys. Rev. Lett., 88: 151602-151602.
PubMedDirect Link - Nair, V.P. and A.P. Polychronakos, 2001. Quantum mechanics on the non- commutative plane and sphere. Phys. Lett. B, 505: 267-274.
CrossRef - Zhang, J.Z., 2004. Fractional angular momentum in noncommutative space. Phys. Lett. B, 584: 204-209.
CrossRefDirect Link








