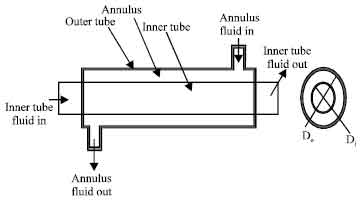
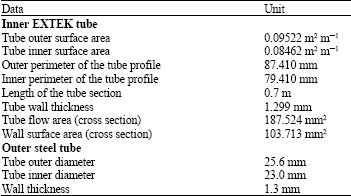
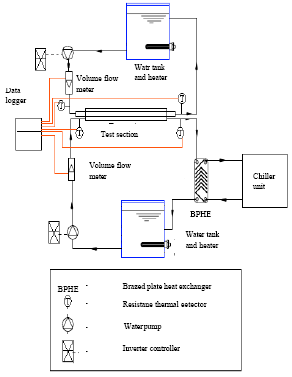
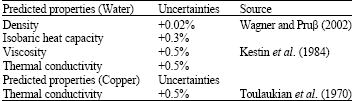
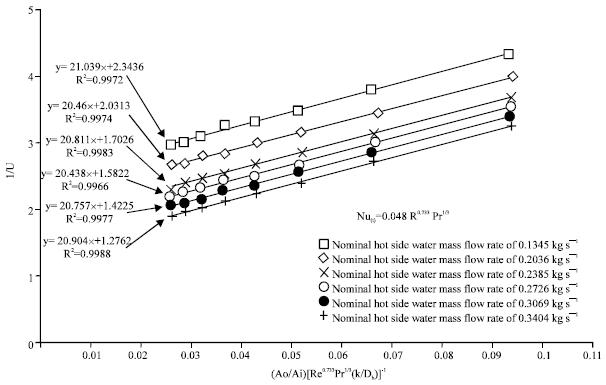
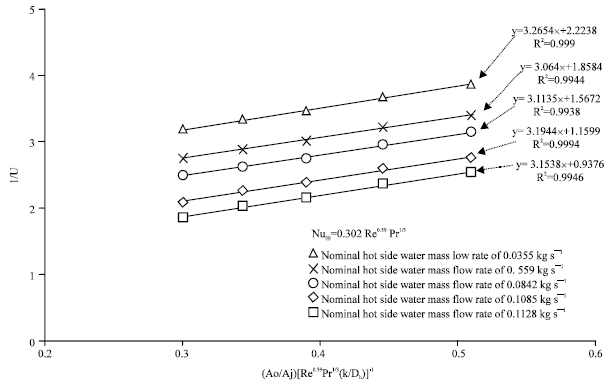
Research Article
The Tube Side Heat Transfer Coefficient for Enhanced Double Tube by Wilson Plot Analysis
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar,31750 Tronoh, Perak, Malaysia
Vijay R. Raghavan
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar,31750 Tronoh, Perak, Malaysia