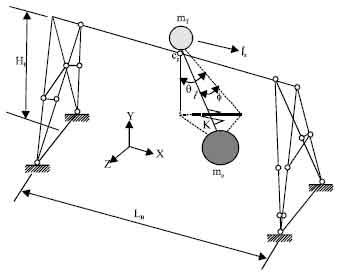
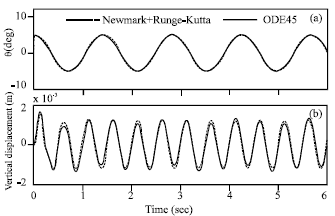
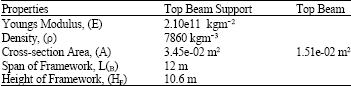
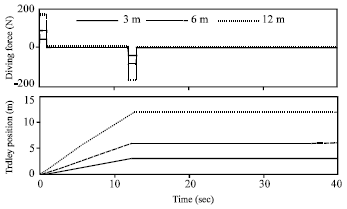
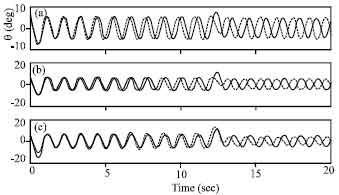
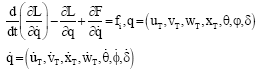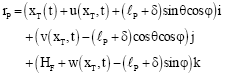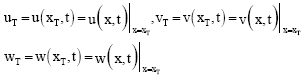Research Article
Open-Loop Responses of Flexible Gantry Crane System
Department of Mechanical Engineering, Universiti of Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Setyamartana Parman
Department of Mechanical Engineering, Universiti of Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Khairul Fuad
Department of Mechanical Engineering, Universiti of Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia