Research Article
Vibration Analysis of Flexible Gantry Crane System Subjected Swinging Motion of Payload
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
S. Parman
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
K. Fuad
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia









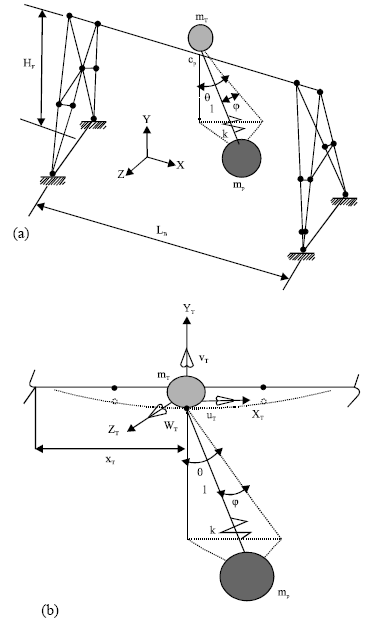
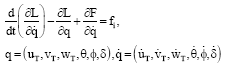
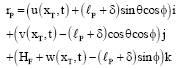
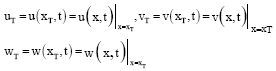

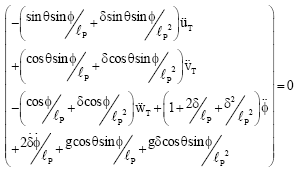

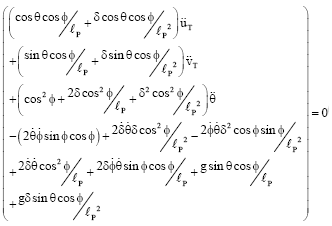

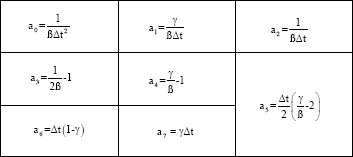
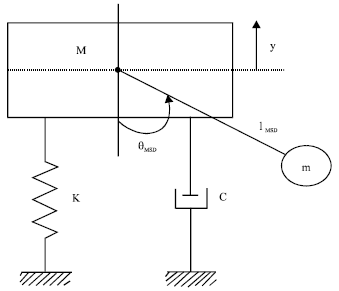
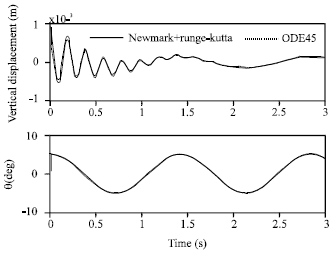




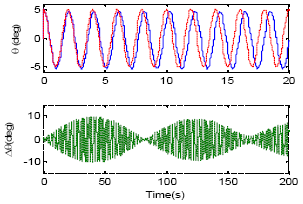
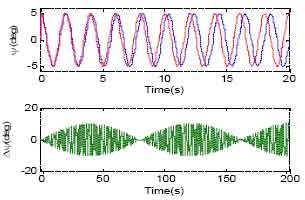
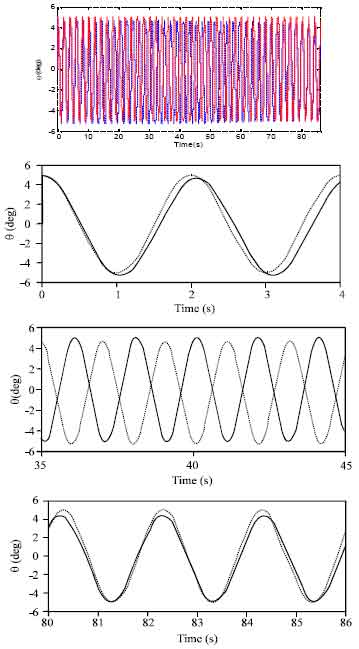
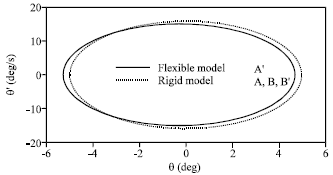
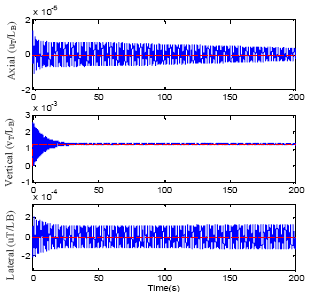
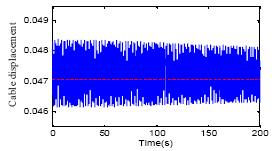
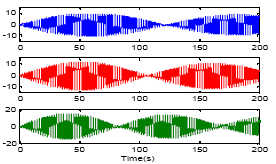
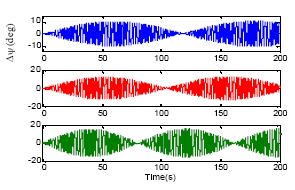
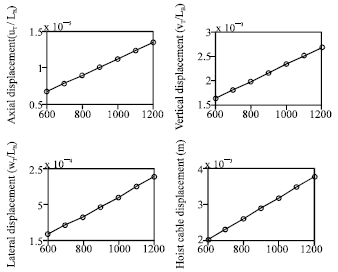
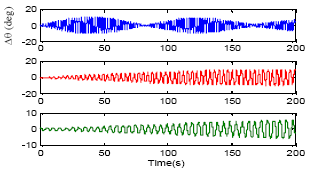
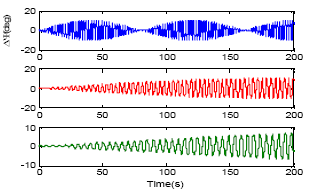

yogesh Reply
i like tihs text very much because it provide me the full knowledge of the crane