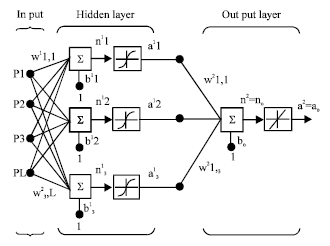
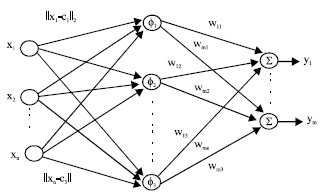
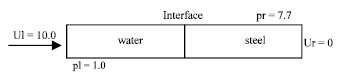
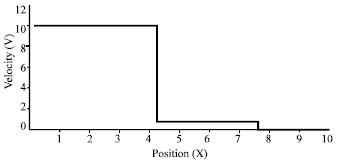
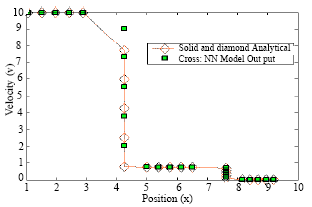
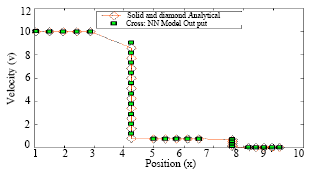
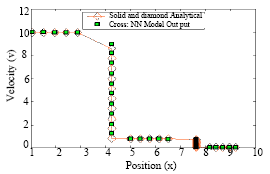
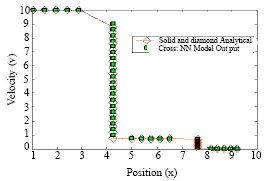
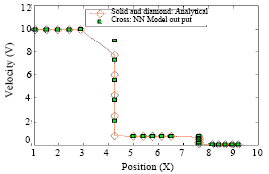
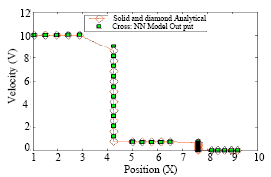
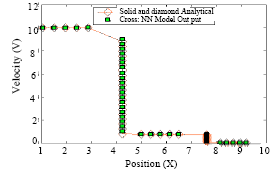
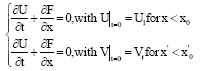Research Article
Model of Neural Networks with Sigmoid and Radial Basis Functions for Velocity-field Reconstruction in Fluid-structure Interaction Problem
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak Darul Ridzuan, Malaysia
Bambang Ariwahjoedi
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak Darul Ridzuan, Malaysia