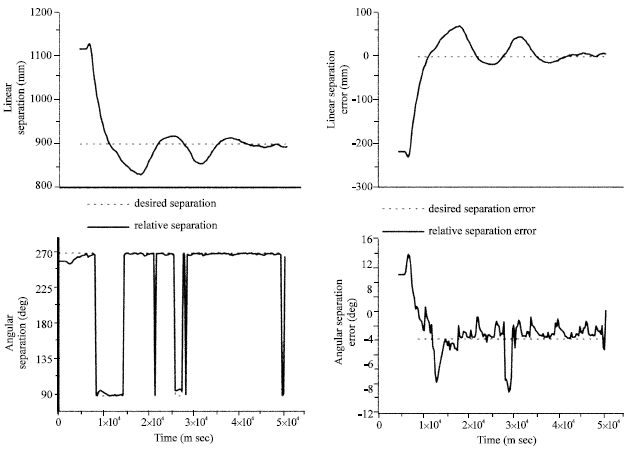
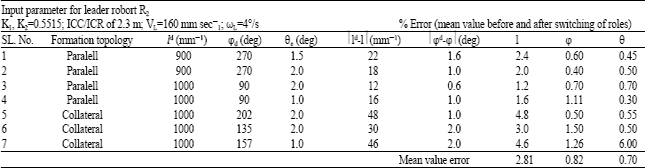
Research Article
Distributed Formation Planning and Navigation Framework for Wheeled Mobile Robots
Precision Engineering and Instrumentation Laboratory, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai, 600036, India
M. Singaperumal
Precision Engineering and Instrumentation Laboratory, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai, 600036, India
T. Nagarajan
Department of Mechanical Engineering Department, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia