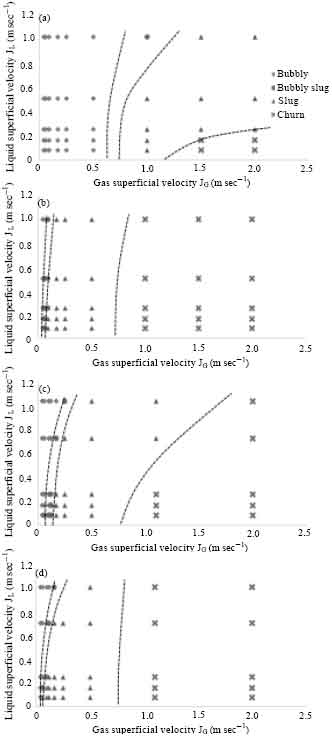
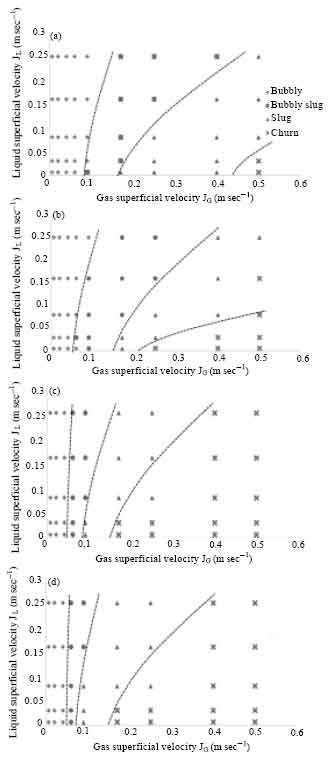
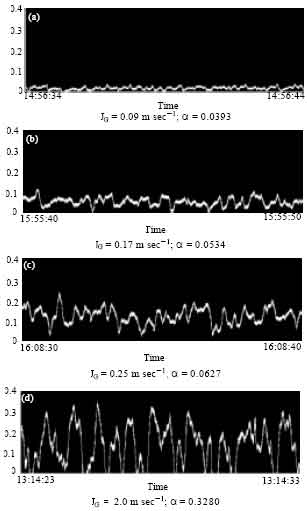
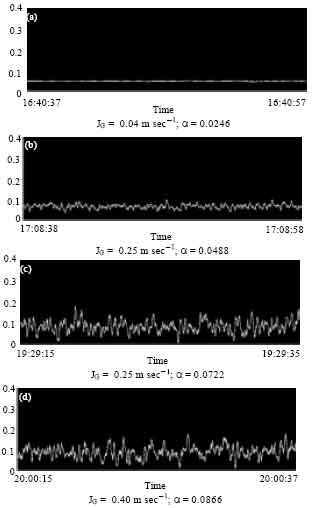
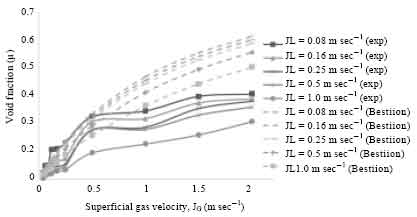
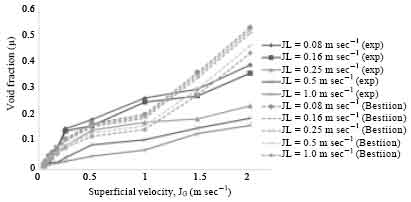
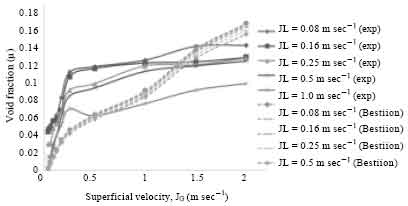
Research Article
Two-Phase Flow Behaviour and Pattern in Vertical Pipes
Department of Mechanical Engineering, Faculty of Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia
M. Z. Zainon
Department of Mechanical Engineering, Faculty of Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia