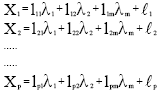
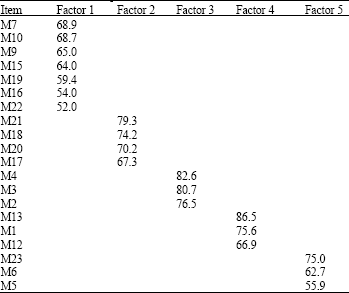
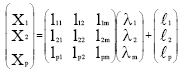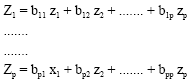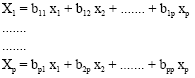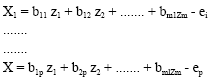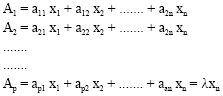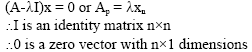Research Article
Factor Analysis Evidence in Describing Consumer Preferences for a Soft Drink Product in Malaysia
Department of Mathematics, University of Malaysia, Terenggganu, Malaysia
Hasliza Asngari
Department of Mathematics, University of Malaysia, Terenggganu, Malaysia