Research Article
Seismic Evaluation of Middle Span Steel I-Girder Bridges
Behbahan Higher Educational Complex, Iran
S. Mohammadsadegh
Behbahan Higher Educational Complex, Iran
Vital applicability, made bridges play a major part in the urban facilities particularly, after destructive earthquakes and its damages can cause serious problems for the residents. It is why seismic evaluation of the bridges has special status and significance economically and socially as well.
In the other hand, bridges are simple structures with small (or zero) degrees of indeterminacy. In the simple structural systems, despite the simplicity in response estimation, failure of a structural member or a support can lead to catastrophic disasters. Thus, they are sensitive systems that even small errors in construction can cause incompensable losses (Thimmhardy et al., 1995). Today, wonderful breakthrough in the field of computer science has made possibilities for simulation and analysis of large models (Arabzadeh and Varmazyari, 2009).
According to Xuewei et al. (2008) it is inevitable to use FEM despite its time ineffectiveness. They also recommended dynamic analysis method. Yet, a number of researchers recognized performance based method as the best designing method (Sung et al., 2009; Zahrai and Bruneau, 1999). In addition to these methods that mostly use in academic contexts, Simplified and approximative methods are usually used in practice. The advantage of the recent method is that they are simple and time effective. This study has been done to answer the following questions:
| • | Are simplified and approximative methods accurate to design? |
| • | Is it necessary to use advanced methods to design regular bridges? |
A number of studies have been done on small scale models of bridge parts (Qaqish, 2006; Sutan et al., 2003; Al-Darzi and Chen, 2006). However, there is no comprehensive work on large scale bridge.
This study aims to evaluate bridge seismic analysis methods, accuracy of code simplified procedures and show the ability and imperfections of each method. We also examine the performance based control method. Here, two large finite element models of steel I-girder bridge in ANSYS software have been constructed. Later, modal analysis was performed to obtain dynamic properties of the bridges. Also, in the second case; they were applied as a basis for other analysis.
In the second step, the results of spectrum analysis, dynamic time history analysis (linear and nonlinear) and nonlinear static analysis (push over) were compared. The modal analysis was employed in order to find the performance point in the push-over analysis results.
MODELING AND ANALYSIS
The first model
The first model description: This steel I girder bridge with 60 m length and 8 m width has two spans. Each girder is supported on a steel pier with rigid connection. Piers-foundation connections are simple. Piers are 6-m high. Concrete slab with 0.2 m thickness has combined interaction with steel girders. This slab in transversal direction has 1 m cantilever part in each side. Table 1 shows sections properties. As shown in Fig. 1, in longitudinal direction, the bridge lay on simple supports that are common in middle span steel bridges (Chen, 1996). Each of these supports is fixed in transversal direction (there is no transversal movement). According to these features the most common types of highway bridges are used (Chen, 1996). Grillage model and its analysis results of this bridge are shown in Fig. 2 and Table 2, respectively (Dicleli, 2002).
The ability to model finite element, rich elements library and performing different dynamic analysis, ANSYS software was used. SOLID65 and SHELL43 elements were used for modeling concrete slab and steel beam, respectively. It should be noted that BEAM24 element can be used for steel beam and column with the advantages in convergence and degrees of freedom. But in beam modeling, it makes some problems in connection with slab. Modeling assumptions are as follow:
| • | Abutments are not modeled because of the |
| • | Volume of the calculations (time and output volume) | |
| • | Abutments are too stiff to have effective role in transversal displacement (Barth and White, 1998) |
| • | Surrounding soil is not modeled. |
| • | Beams are assumed to have full connection with slab. And there is no sliding between them. |
| • | Live loads are not considered in seismic analysis (Ghosn et al., 2009). |
Modeling: Concrete slab are modeled with 16*120 of SOLID65 elements. Volume of each element is equal to 0.2x0.5x0.5 m3. Beams' webs and flanges are modeled using 4x2x2x120 and 4x2x120 SHELL43 elements, respectively. Columns web and flange are modeled using 4x2x12 and 4x2x2x12 previous elements (SHELL43), respectively.
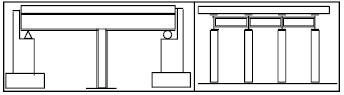 | |
| Fig. 1: | Elevation of the bridge-first model |
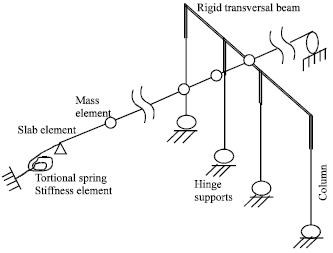 | |
| Fig. 2: | DICLELI model (Dicleli, 2002) |
| Table 1: | The first bridge member dimensions (according to CISC code) |
| Table 2: | Grillage model results (Dicleli, 2002) |
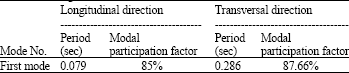 | |
| Table 3: | The results of FEM modal analysis |
This element is highly recommended for modeling of beams and columns' web, flange and stiffeners (Barth and White, 1998). Figure 3 shows FEM model of bridge.
Beam and column connections are rigid. In roller support longitudinal movement and rotation about all axises is possible. In hinge support rotational stiffness are modeled using a COMBIN 14 element. Properties of this element are extracted from grillage model (Dicleli, 2002).
Modal analysis: The Modal analysis (free vibration) results are shown in Table 3. It should be noted that this analysis is linear and elastic. First mode shapes in transversal and longitudinal direction are shown in Fig. 4.
 | |
| Fig. 3: | FEM model of first bridge |
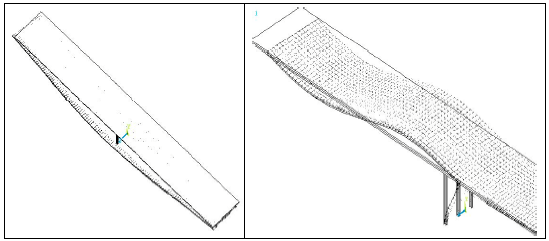 | |
| Fig. 4: | First mode shapes in transversal and longitudinal direction |
Results comparison: The results (Table 4) showed a slight difference between two simulation methods. The most remarkable causes for these differences are as follow:
| • | In grillage model the dock is modeled as rigid body and hence, the dock torsion effects were not noticed in transversal direction. However, The period and participation factors change |
| • | Tension and compression effects were not considered in transversal direction. These simplifications can decrease the transversal period due to the neglection of some dock mode or increase in the participation factor of the first mode |
| • | In the grillage model mass is modeled concentrically. Hence, the number of effective modes is limited in this analysis. But in finite element model about 47000 modes can affect the vibration. In general, more simplifications in grillage model cause these differences |
It is evident that simplified models are not as accurate as finite element models. Thus some authors recommend finite element models, ignoring its time ineffectiveness.
| Table 4: | FEM modal analysis and grillage results comparison |
 | |
It should be noted that FEM model has used some simplifications. such as, the interactive modeling of beam and slab and beam and column connections or supports. Hence the grillage model is able to estimate structure dynamic properties accurately.
The second model: This model is similar to the first model but its width is 4 m and it has 2 piers. According to pre-mentioned properties it has 25000 degrees of freedom. Supports are modeled like the first model according to the Barth and White (1998) recommendations.
Modal analysis: To calculate the period, the modal analysis of FEM model second bridge in ANSYS software was done and 30 vibration modes were studied.
In transversal direction, the first free vibration mode contains (period = 0.49 sec and participation factor = 131403/153590 = 0.86) 0.86 of the mass and the third mode consists of (period =0.11 s and participation factor = 19033/153590 = 0.12) 0.12 of the mass.
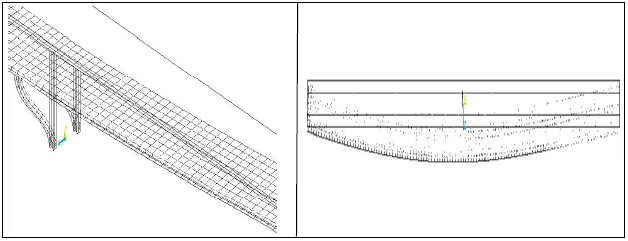 | |
| Fig. 5: | FEM transversal and longitudinal displacements |
| Table 5: | Comparison of bridge vibration using different codes |
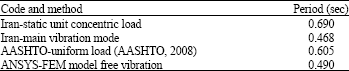 | |
These two modes possess 0.86+0.12 = 98% of total mass (bridge period calculated according to Iranian and ASHTO Codes). The results are given in Table 5.
| • | According the Fig. 5, the results showed that in transversal direction, one mode has the greatest amount of participation factor (higher than 0.85) and governed the vibration. According to ASHTO and CALTRANS (SDC) Codes this bridge is regular (normal). So, it suffices to consider one mode in analysis |
| • | In transversal direction the results differ greatly, because of different kinds of supports in the sides and consequently, asymmetry of bridge |
Due to two bridge-sides' constrains in transversal direction, the mid point has maximum displacement. Thus, using mid point displacement in calculations (according to the Codes) leads to less stiffness and longer period. Also applied force to this point makes maximum displacement. In ASHTO Code, it is tried to solve the problem by identifying distributed load. That reduces the period (Table 5). In single mode methods (AASHTO, 2008), improving the load pattern and location of displacement measurement cause even more shortening in the period.
Dynamic time history analysis: Dynamic time history analysis is the most accurate method for structures seismic evaluation (Sakai and Unjoh, 2006). One of the most challenging steps in this analysis is selecting the proper ground motion.
Linear analysis: Linear dynamic analysis acceleration with a time step of 0.005 sec. was applied to the base of the structure. Linear properties of materials were considered according to the part one of the bilinear curve of Fig. 6. The given ground motion was scaled ElCENTRO acceleration with site design spectrum. The analysis and modeling assumptions were explained previously. The duration of the analysis was about 6 h, output volume (contain stresses, strains, displacements and supports reactions) is about 4 GB.
Non-linear analysis: This analysis is known as the most accurate procedure and so it can release exact information about seismic properties. Non-linear properties of the materials are visible in Fig. 6a and b. But regarding the linear analysis of results (small displacements), geometric non-linear effects were not used. Strong ground motion is like linear analysis. The duration of this analysis with given assumptions was about 13 h and the out put file volume is about 7 GB.
Spectral analysis: As mentioned earlier, smooth spectrum of scaled ELCENTRO earthquake was used for spectral analysis. In order to obtain the spectrum the EERA software was applied. This spectrum was applicable in EXCEL software. CQC and SRSS combination methods are used for calculations.
Push-over analysis: Push-over analysis conducted by lateral loading in an increasing pattern basis. Selecting accurate pattern of lateral loading in this analysis is of highly significance. But there is no single way to solve the problem (Sun and Su, 2009). However, slight changes in load pattern can not influence the results greatly.
 | |
| Fig. 6: | Stress (MPa)-strain relationship in (a) steel and (b) concrete |
One of the most popular ways of loading is according to the first mode-shape. Push-over analysis needs model dynamic properties.
Regarding dynamic analysis information we learned that there is no correlation between dominant transversal and longitudinal modes. Thus, push-over analysis can be done in each direction separately.
Increase in lateral loading and member yielding cause stiffness reduction. Non-linear force-displacement proposes system characteristic (capacity) curve. The duration of the analysis is 100 h.
Push-over analysis results processing: Push-over analysis results processing has been done using different methods. One of these methods is C.S.M. in which maximum structural displacement estimation is the intersection of structural capacity and seismic design spectrums.
Regarding the high degrees of freedom and unusual vibration shape (compared with buildings) the above mentioned method is not accurate and reliable in this case.
It seems that using modal analysis can solve the problem. First equivalent one degree of freedom system (eof) characteristics should be determined. Varies methods are available for finding eofs characteristic.
| (1) |
| mSDOF | : | Equivalent mass of single degree of freedom (SDOF) |
| φ(x) | : | First mode shape |
| m(x) | : | System mass per length |
Finding relation between force and displacement of SDOF system, we use Eq. 2:
| (2) |
| (3) |
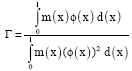 | (4) |
where, SSDOF and FSDOF are displacement and force of SDOF respectively and DMDOF and FMDOF are these characteristics for multi degrees of freedom (SDOF) system that obtained using push over analysis.
Γ is modal participation factor obtained from normalized mode-shape function (φ). Γ is equal to PF1. This factor is considered as a scaling factor.
Bilinear elastic system period is calculated using following equation:
| (5) |
where, DYSDOF and FYSDOF are displacement and yielding stress of equivalent bilinear elastic system.
Obtaining capacity spectrum in AD format (spectral acceleration v.s displacement), Sa is calculated as:
| (6) |
And for writing response spectrum (Sa vs. T) in ADRS format (Sa vs. spectral displacement) we can use:
| (7) |
Considering these equations we have longitudinal First mode-shape φ(x) = 2x10-8 x3 -5x10-6 x2 +0.0003x+ 0.0002 that can be normalized like below (φ(x)max = 1).
 | |
| Fig. 7: | Performance point of second model |
So
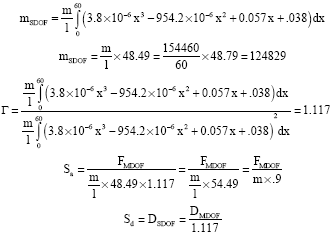 |
the performance point of the bridge obtained in Fig. 7.
| • | Displacement analysis results showed a slight stress and strain in slab. That is because of the bridge design rationale (strong beam (slab) and weak column), which is in line with Dicleli (2002), who modeled I-girder bridges using grillage model and concluded slight displacement in bridge decks |
| • | In the spectral analysis, there was a great correlation between the results of two combination method. Regarding this point that modeled bridges are regular systems, it has been predictable and are in agreement with Wilson and Kureghian (1981) |
| • | In the time history analysis results are in good agreement with spectral analysis. Regarding duration and output volume in time history analysis, spectral analysis is recommended by author. Where as, Xuewei et al. (2008) recommended time history analysis regardless of cost ineffectiveness of the method |
| • | Push-over analysis results showed great differences with other methods that can be the results of load pattern. The load applied to the center of gravity for simplicity in codes. In the pervious section we saw such a difference between periods in different methods (period ratio and displacement ratio). These results seem to be reasonable. Some researchers advised this method without noticing the load pattern. However in recent studies this issue has been considered in bridges analysis (Sung et al., 2009) |
The following tips can be concluded:
| • | Regarding time effectiveness, the researcher recommends Spectral analysis and code method |
| • | In push-over method it seems necessary to apply distributed load in transversal direction since concentric loading makes great errors |
| • | In simplified code method, desirable results can be obtained if loading is distributed in bridge span; hence load pattern in some codes needs some modifications |
| • | Regarding the time consuming process, practical difficulties and the results' similarities in various analysis, There is no need for non-linear analysis in regular middle span bridges |