Research Article
Solution of Pseudoparabolic Equation by Finite-Element Method
Department of Mathematics, Azad-University of Ilam, Iran
A. Farmany
Department of Mathematics, Azad-University of Ilam, Iran
Let, Ω⊂Rn be a bounded domain with the smooth boundary and t>0.
The following initial-boundary value problem (Showalter, 1996):
| (1) |
| (2) |
| (3) |
Where:
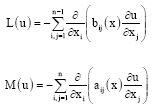 |
and bij(x) = bji(x), aij(x) = aji(x) (i,j = 1,2,...,n) are continuous functions in ![]() and the following inequality is valid:
and the following inequality is valid:
For ∀x ∈ ![]() , ∀ξ ∈ ℝn was investigated by Petrosyan and Hakobyan (2008).
, ∀ξ ∈ ℝn was investigated by Petrosyan and Hakobyan (2008).
The problem in Eq. 1-3 was investigated in the case in which L is linear, M is nonlinear where, L and M are degenerated operators (Petrosyan and Hakobyan, 2008). The solution of a general case in which L and M are nonlinear is considered by Gaevskii et al. (1978). Quarteroni et al. (2000) proved (using Galerkin’s method) that the solution of the problem 1-3 exists (Mamikonyan, 2006).
In this study, we construct an approximate solution of the problem 1-3 using finite-element method for the case in which Ω∈(0,1)x(0,1)⊂ℝ2, Lu = -Δu,
Definition: The function:
may be a weak solution of the problem in Eq. 1-3 if:
and for:
the Eq. 4 is valid:
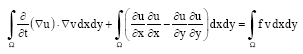 | (4) |
Petrosyan and Hakobyan (2008) proved that the Eq. 4 has a unique solution.
Let, we construct an approximate solution for the problem in Eq. 4 using the finite-element method.
Suppose the partition domain Ω = (0,1)2 with a uniform triangulation of mesh size h with respect to x and y as Fig. 1.
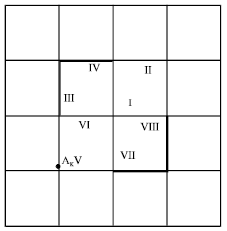 | |
| Fig. 1: | Partition domain Ω = (0,1)2 with a uniform triangulation of mesh size h with respect to x and y |
xi+1 -xi = h,i,j = 1,2,...,n, yj+1-yj = hh = 1/n |
We construct the piecewise linear functions φij(x,y) by the following rule:
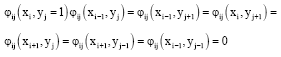 |
and linear in the domain of every triangle. In the remained triangles of the square [0,1]x[0,1] we assume φij (x,y) = 0.
In continue, we set N = (n-1)2 as the basis functions. Let, ωn = {(ih, jh); i, j = 1,2,...,n-1}. If we number the points of the set ωn for example:
then, the basis functions φij will be renumbered, i.e., by constructing ψk(Ar) δkr (k,r = 1,2,...,n-1) we get the system ψ1,ψ2,...,ψn.
Note that Sn is the linear space generated by the functions ψi = (i = 1,2,...,N) and dimSn = N and ![]() where, v is linear in every triangle and v = 0 on ∂Ω}.
where, v is linear in every triangle and v = 0 on ∂Ω}.
It is easy to see that:
is a subspace. To calculate,
we use the Table 1.
| Table 1: | The derivatives of the basis functions ψi |
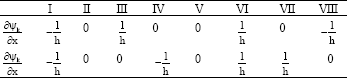 | |
Denote:
To find the weak solution of the problem 1-3 we use the Galerkins method:
 |
which is equivalent to:
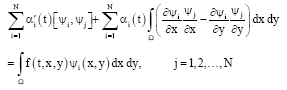 | (5) |
We can rewrite the Eq. 5 in the matrix form:
| (6) |
where, βN = (α1,α2,...,αN),
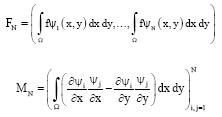 |
It is easy to check that the matrix MN has the following form:
 |
where, E is the unit matrix and A is the following matrix of order of (n-1)x(n-1):
 |
The solution of the system of differential Eq. 6 with the conditions:
| (7) |
where, ci are the coefficients of the expansion of the function u0(x,y) by the basis ψi(x,y) (i =1,...,N) may be denoted by using αi(t) (i = 1,...,). Thus, we obtain the following sequence of the functions:
This sequence:
converges in:
norm to the weak solution of the problem in Eq. 1-3.
To find the numerical solution of the system 6 we use the θ method (Braess, 2001). Suppose the partition [0,T] into equal parts with the step Δt denote by:
Now we replace the system 6 by the following different system:
| (8) |
where, ![]()
For every k, we get the linear system of equations.
We choose the parameter θ such that the matrix:
will be positive,
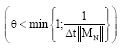 |
Then we can represent the system of Eq. 8 in the following form:
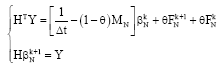 | (9) |
where, K = HTH.
Denote by:
It is easy to verify that:
The initial boundary value problem is investigated for the pseudoparabolic equation with nonlinear operators. An approximate solution for this problem is obtained using the finite element method. Finally it is proved that the constructed sequence converges to the exact solution is possible.