ABSTRACT
Let (S, τS) be a topological semigroup. In this note, we study the notion of topological congruences on topological S-acts, i.e., for a topological S-act (A, τ), when A/θ with the quotient topology is a topological S-act. Let (A, τ) be a topological S-act (S-flow) and θ be an S-act congruence on A (a semigroup congruence on S) and let Lθ be the lattice of closed subsets, relative to the closure operator Cθ. As the main result of this study, we prove that θ is a topological congruence on (A, τA) (resp., (S, τS)) if and only if (A, τA ∩ Lθ) (resp., (S, τS ∩ Lθ)) is a topological S-act (a topological semigroup). Also, we prove that when Y is closed, the study of Rees congruence ρY is related to the study of the lattice of open sets which contain Y.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2010.766.771
URL: https://scialert.net/abstract/?doi=jas.2010.766.771
INTRODUCTION
Topological semigroups, their actions, their representations and topological congruences over them have been studied by many mathematicians and have a very wide usage in many fields like topological vector spaces, geometry or analysis. More specially, there are many works about topological Rees congruences on semigroups and there are some works about the congruences on S-flows which are compact topological S-acts (Berglund et al., 1989; Gonzalez, 2001; Gutik and Pavlyk, 2006; Hryniv, 2005; Lawson and Lisan, 1994; Lawson and Madison, 1971; Normak, 1993, 2006).
As the first step in the study of the category of topological S-acts, in this note, we study the notion of topological congruences on topological S-acts. This study can be used in the study of universal objects like push out or coequalizer. Here, we briefly state the notions and definitions which will be used in present study about topological S-acts and their congruences. Next, we will state a criterion for detecting topological congruences on topological S-acts and as well, on topological semigroups. As an application of the results, we give a necessary and sufficient condition for a longstanding problem raised by Wallce (1955). Later we will give a better criterion for Rees congruence ρB on a topological S-act (A, τA) where, B is a closed subact of A. As a part of this section, we will prove that if B is a closed compact or clopen subact of (A, τA), then the Rees congruence ρB is a topological congruence on (A, τA).
Recall that, for a semigroup S, a set A is a left S-act if there is, so called, an action λ: SxA→A such that, denoting λ (s, a): = sa, (st) a = s (ta) and, if S is a monoid with 1, 1a = a (for more information about S-acts, (Ebrahimi and Mahmoudi, 2001; Kilp et al., 2000).
A semigroup S with topology τS is a topological semigroup if the multiplication μ: SxS→S is (jointly) continuous, where SxS has product topology. We denote such a topological semigroup by (S, τS).
For a topological semigroup (S, τS), a (left) topological S-act is an S-act A with a topology τA on it such that the action λ: SxA→A is jointly continuous. (Note that SxA is considered with product topology). If A with a topology τA is a topological S-act, we simply denote it by (A, τA).
Since, in our study, we need to discuss on one S-act or one semigroup with different topologies, we use this terminology to prevent misunderstanding. We denote the category of all left topological S-acts with continuous S-homomorphisms between them with S-Top.
Recall that for a semigroup S and an S-act A, the functions λs: A→A is defined by y→sy for any yεY. Similarly for any aεA the function ρa: S→A is defined by y→sa. Since, in some of our results we need to talk about λs: A→A and λs: A/θ→A/θ at the same time, to prevent misunderstanding, we show the latter by Λs: A/θ→A/θ.
Now, if S has a topology τS for which its multiplication SxS→S is (separately) continuous, that is, λs and ρs are continuous for all sεS, then S with this topology is called a semitopological semigroup (for more information about semitopological semigroups (Berglund and Hofmann, 1967; Wolfgang, 1984).
Similarly, one can define a semitopological S-act by taking λs: A→A and ρa: S→A to be continuous for each sεS and aεA (Khosravi, 2009).
We say a topological semigroup (S, τ) has (left) ideal topology, if any open set in S is a (left) ideal of S (this definition is more general than what is implied by Normak (1993). Similarly, a topological S-act (A, τA) has subact topology, if any open set in A is a subact of A.
A semigroup topological congruence on a topological semigroup (S, τS) is a semigroup congruence θ (that is, if sθsi where, s, siεS, then for any tεS, tsθtsi and stθsit) such that the semigroup S/θ with the quotient topology is a topological semigroup.
For an S-act A and a congruence θ on it, we denote the usual quotient map from A to A/θ by π. By a zero in an S-act A, we mean an element aεA such that for any sεS, sa = a. For an S-act A, by P (A) we mean the powerset of the underling set of A.
By a clopen subset in a topological space, we mean a closed and open subset in that space. In this study, for any subset C of a topological space X, by cl(C) and int(C), we mean the closure of the set C in X and the interior of C in X, respectively. By a descending chain of open subsets in a topological space, we mean a collection of open sets which is induced by a totally ordered set J such that for all α, βεJ, if α≤β, then Oα⊇Oβ.
S-ACT TOPOLOGICAL CONGRUENCE
An S-act topological congruence or when there is no ambiguity about S-act, briefly, a topological congruence on a topological S-act (A, τA) is an S-act congruence θ (that is, if aθai for a, aiεA, then saθsai for all sεS) such that the S-act A/θ with the quotient topology is a topological S-act.
Remark 1: Considering a semigroup S as an S-act, any semigroup congruence is an S-act congruence, but the converse is not true in general. However, there are topological semigroups, namely S with some congruence θ such that θ is not a topological semigroup congruence while θ is a topological S-act congruence.
Let, (A, τA) be a topological S-act and θ be a congruence on A. The following is a closure operator on A (Burris and Sankappanavar, 1981; Dikranjan and Tholen, 1995).
A subset X of A is called a closed subset, (relative to Cθ), if Cθ (X) = X. Consider the lattice of closed subsets relative to Cθ and denote it by Lθ (Lθ = {B ⊆ A|Cθ (B) = B}). Since, Lθ is a sub-Boolean algebra of P (A), it obviously forms a topology on A.
Remark 2: Note that for a topological S-act (A, τA) and a congruence θ on it, for any open set OετA ∩ Lθ, the image O under the map π: A→A/θ is open in A/θ with the quotient topology.
For any topological S-act (A, τA), the study of a topological congruence θ on (A, τA), depends essentially on the behavior of the original topology τA and the topology Lθ. The following proposition shows this relation.
Proposition 3: Let, (A, τ) be a topological S-act and θ be a congruence on A, then θ is a topological congruence if and only if (A, τ∩ Lθ) is a topological S-act.
Proof: (⇒) Let θ be a topological congruence. Let sεS, aεA and Uετ∩ Lθ with saεU. By Remark 2, π(U) is an open set which contains s[a]. So, there exist open sets Ws and V[a] in S and A/θ, respectively such that sεWs, [a]εV[a] and s[a]εWs·E V[a] ⊆ π(U). Note that the open set π-1(V[a]) contains a and belongs to τ ∩ Lθ and further satisfies sa ε Ws·π-1(V[a]) ⊆ π-1(π(U)) = U, (since UεLθ). So (A, τ∩Lθ) is a topological S-act.
(←) Let (A, τ∩ Lθ) be a topological S-act for some congruence θ on A. We show that A/θ with the quotient topology is a topological S-act.
Let sεS, [a]εA/θ and U in A/θ are given such that s[a]εU. So saεπ-1(U) and we know that π-1(U)ετ∩ Lθ, so by the assumption, there exist open sets Vaετ∩Lθ and Ws such that aεVa, sεWs and saεWs· Va ⊆ π-1 (U).
Since Vaετ _∩ Lθ, by Remark 2, we have π(Va) is open in A/θ. So s[a]εWs · π(Va) ⊆ π(π-1(U)) = U, (since π-1(U)ετ∩ Lθ).
By a similar argument as in the proof of Proposition 3, (1) and (2) we get the semigroup congruence version of the above proposition which is a necessary and sufficient condition for this question raised by Wallce (1955) that when the quotient semigroup S/θ is topological.
Proposition 4: Let (S, τS) be a topological semigroup and θ be a semigroup congruence on it. Then the following are equivalent:
| • | θ is a semigroup topological congruence |
| • | (S, τS ∩ Lθ) is a topological semigroup |
Since, the next proposition can be proved easily, we state it without proof.
Proposition 5: Suppose that (A, τA) is a topological S-act and θ is a congruence on A. If π: A→A/θ is an open map, then θ is a topological congruence.
Note that we have the following property for any congruence θ on A.
Proposition 6: (Khosravi, 2009): Let (A, τA) be a topological S-act. Then for every congruence θ on A, we have:
| • | For all sεS, the map Λs: A/θ→A/θ defined by [a]→s[a] is continuous |
| • | For all aεA, the map ρ[a]: S→A/θ s→s[a] is continuous |
As a quick consequence of the above proposition, we have:
Corollary 7: For any topological S-act (A, τA) and any congruence θ on A, A/θ with the quotient topology is a semitopological S-act.
Remark 8: Since, the lattice of closed subsets relative to a closure operator is closed under arbitrary intersections, if (A, τA) is an Alexandroff topological S-act, then for any congruence θ on A, (A, τA ∩ Lθ) is an Alexandroff space. By the definition of the quotient topology, this implies that A/θ with the quotient topology is an Alexandroff space.
Corollary 9: Let (A, τ) be an Alexandroff topological S-act and θ be an arbitrary congruence on A. Then θ is a topological congruence and A/θ with the quotient topology is an Alexandroff topological S-act.
Proof: Since for an Alexandroff topological S-acts, the joint continuity and separately continuity of the action is equivalent (Khosravi, 2009) θ is a topological congruence by Corollary 8 and A/θ is Alexandroff. As a quick result of the above proposition, we have:
Corollary 10: Let S-Alex be the category of all Alexandroff topological S-acts with continuous S-homomorphisms between them. Then S-Alex is closed under quotient. Similar to Proposition 9, we have:
Proposition 11: Let (S, τS) be an Alexandroff topological semigroup and (A, τA) be a topological S-act and θ be an arbitrary congruence on A. Then θ is a topological congruence.
Corollary 12: For an Alexandroff topological semigroup (S, τS), S-Top is closed under quotient and it is complete and cocomplete.
REES TOPOLOGICAL CONGRUENCE
Here, we study the Rees congruences on topological S-acts and on topological semigroups. In fact, in this section, we consider this question: for which subact Y of a topological S-act (A, τA), the Rees congruence ρY is a topological congruence?.
In the rest of this note, suppose that (S, τS) is a topological semigroup. For a topological S-act (A, τA) and its closed subact Y, first we give necessary and sufficient conditions for this question. Then by using these conditions, in some cases like when the lattice of open sets which contain Y, has a minimum element, or when (S, τS) is locally compact or Alexandroff, we answer to this question.
Notation 13: From now on, we denote the lattice LρY by LY for simplicity. Similarly, we denote the operator CρY by CY. Also, for a topological S-act (A, τA), by a Rees quotient space, we mean the quotient space A/Y, for some subact Y.
Remark 14: As a quick consequence of Corollary 9, we can easily conclude that every Rees congruence on a topological S-act (A, τA) where (S, τS) is an Alexandroff topological semigroup, is topological.
Since by Proposition 3, for any topological S-act (A, τA), the study of congruence ρY on A depends on the structure of the lattice τA∩ LY before we continue present study in this section, we explain this structure in the following.
Remark 15: For a topological S-act (A, τA) and a subact Y of it, the elements of τ ∩ LY are:
| • | Open sets which contain Y |
| • | Open sets which are disjoint from Y |
We are going to study the S-act Rees congruence ρY where Y is a closed subact. For this purpose, we divide our discussion to the following cases:
| • | Y is a closed compact subact |
| • | Y is a closed subact and the lattice of open sets in τA∩LY which contain Y, has a minimum element |
| • | Y is a closed subact and there exists a chain of open sets in τA∩ LY around Y which has no minimal element |
Then, we state and prove an equivalence condition which can be used in all of these cases. Then, by using this tool, we characterize topological Rees congruences in the first and the second case exactly. For the third case, we answer the question in some cases with extra assumptions.
Before we state the next proposition in this section, we need the following notation.
Notation 16: For an S-act A and two subsets U and V of A, by (U: V), we mean the following set:
(U:V): = {sεS|sV⊆U } |
Now, we state the Rees congruence version of Proposition 3 for a closed subact, which simplifies present study in future.
Proposition 17: Suppose that Y is a closed subact of a topological S-act (A, τA). Then the following are equivalent:
| (i) | ρY is a topological congruence. |
| (ii) | For each open set U in A which contains Y, there exists a family of open subsets of U like {Vα }αεJ such that each Vα contains Y and {int((U: Vα))}αεJ is an open covering for S. |
| (iii) | Considering A with topology τA∩LY, the action λ: SxA→A, is continuous at any point (s, y) where, yεY and sεS. |
| (iv) | The action of A/Y is continuous at any point (s, [y]ρY) where yεY and sεS. |
Proof: (1)⇒(2) Suppose that ρY is a topological congruence. By Proposition 3, (A, τA∩LY) is a topological S-act, so for any arbitrary aεY, sεS and UετA∩LY such that saεU, there exist open sets Va,sετA∩LY and WsετS which contain a and s, respectively such that saεWs·Va,s⊆U. Now note that since Y is an S-act and aεY⊆Va,s, then saεVa,s. Therefore without lose of generality, we can assume that Va,s ⊆ U. Consider the family {Va,s }sεS which is found by the above discussion. Since aεVa,s for any sεS and aεY, by Proposition 15, Y⊆Va,s for any sεS. Note that for any sεS, int((U: Va,s)) contains Ws. So, obviously {int((U: Va,s))}sεS is an open covering for S.
(2)⇒(3) We prove this part by Proposition 3. Suppose that we are given aεA and sεS and UετA∩LY such that saεU. By hypotheses, there exists an open covering {int((U: Vα))}αεJ for S such that for all αεJ, Vα contains Y. So, there exists a β such that sεint((U: Vβ)). We have obviously VβετA∩LY and saεint((U: Vβ))·Vβ⊆U.
(3)⇒(4) Suppose that we are given yεY, sεS and an open set U in A/Y such that s[y]εU. Obviously π-1(U)ετA∩LY and syεπ-1 (U). By hypothesis, there exist Ws and VyετA∩LY which contain s and y, respectively such that syεWs ·Vy ⊆ π-1 (U). By Remark 2, π(Vy) is open in A/Y and syεWs · π(Vy) ⊆ U.
(4)⇒(1) According to Proposition 3, we need to prove that (A, τA∩LY) is a topological S-act. Suppose that aεA, sεS and UετA∩LY are given such that saεU. Since (A, τA) is a topological S-act, there exist open sets Va and Ws which contain a and s, respectively such that Ws·Va⊆U. If a∉Y, then define O = Va∩(A-Y). By proposition 3, O belongs to τA∩LY which contains a and satisfies:
saεWs· O⊆U |
So the action of A is continuous at every point (s, a) s.t. a is not in Y and sεS. Now suppose that aεY. Since UετA∩LY is a nonempty open set, the set U contains Y and we have obviously π-1(π(U)) = U. Hence s[a]επ(U) where, π(U) is an open set in the quotient topology. By the hypothesis, there exist open sets Ws and V[a] which contains s and [a], respectively and s[a]εWs·V[a]⊆π(U).
Remark 18: Note that if for some topological S-act (A, τA) and two subacts of it, namely Y and Z, the lattices LY∩τA and LZ∩τA are the same, then ρY is topological if and only if ρZ is topological. This fact can be used as a method for studying Rees congruences by relating them to some known topological Rees congruences. We explain this method by the next example.
Example 19: Consider (N∞, min) with topology τ = {Ψ, {N∞}}∪{{1, ..., n}|n≥4}. It is obviously a topological semigroup and for ideals Y: = {1, 2} and Z: = {1, 2, 3}, we have τ∩LY = τ∩LZ. (Since Z is closed and τ∩LZ has minimum element, ρZ is topological by Proposition 28, therefore, by the above remark, ρY is topological).
Proposition 20: Let (S, τS) be a topological monoid with some topology on it such that 1 just belongs to one open set in S. If (A, τA) is a topological S-act and Y is its closed subact, then ρY is topological.
Proof: First note that all of the topological S-acts on this monoid have subact topology. Since (A, τA) is a topological S-act and we have obviously 1a = aεU for any arbitrary UετA and aεU, there exist open sets W1 and Va such that 1aεW1·Va⊆U. But by the assumption, we have W1 = S. So Sa⊆U for all every point (s, a) s.t. a is not in Y and aεU, therefore U is a subact. By Proposition 17 since for any open set U in τA we have (U: U) = S, the congruence ρY is topological.
Similarly, by Proposition 17. one can easily prove that:
Proposition 21: Let (A, τA) be a topological S-act with subact topology. Then for any closed subact Y, the Rees congruence ρY is topological.
As a quick consequence of proposition 20, we have:
Corollary 22: Let (S, τS) be a topological monoid with some ideal topology. Then any Rees congruence ρY for any closed subact Y of a topological S-act is topological.
Proposition 23: Let Y be a compact closed subact of (A, τA). Then ρY is a topological congruence.
Proof: To prove this assertion, we use Proposition 17. In fact we show that if we consider A with topology τA ∩LY, then the action λ: SxA→A is continuous at every point (s, y) where, yεY and sεS. Suppose that we are given sεS, yεY and an open set U which contains Y such that syεU. Since, (A, τA) is a topological S-act, there exist open sets V(y) ετA and W (s, y) ετS which contain y and s, respectively such that:
syεW (s, y)· V (y)⊆ U |
Fixing s and repeating the above argument for any yεY, we reach to the family {V (y): yεY } which is clearly an open covering for Y. Since, Y is a compact subact, there exist open sets V (y1),...,V(yk ) for some kεN such that:
Y⊆ V (y1)∪...∪ V (yk ) |
Let V be the union of V (yi ), for 1≤i≤k and W be the intersection of W (s, yi), for 1≤i≤ k. We have saεW· V⊆U.
Since any closed subset of a compact space is compact, as a quick result of the above proposition, we have:
Corollary 24: Let (A, τA ) be an S- flow. Then for any Rees congruence ρY on A such that Y is closed, the Rees congruence ρY is topological.
Remark 25: Note that if π : X→X/ρ is a quotient map and Z is a locally compact space, then the function πxidZ is a quotient map, too.
Proposition 26: Let (S, τS) be a locally compact topological semigroup and (A, τA) be a topological S-act. Then any congruence θ on (A, τA) is topological.
Proof: Let λ be the action of S on A and θ be a congruence on A. First, note that the following diagram is commutative:
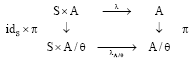 |
where, π: A→A/θ is the natural quotient map. Let O be an open set in A/θ. Since π and λ are continuous, the inverse image of O under π○λ is open in SxA. Define V := (π○λ)-1 (O). Since, S is locally compact, by Remark 25 the function idSxπ is a quotient map and (idS xπ)(V ) is open in SxA/θ. Hence λA/θ is continuous and θ is topological.
Example 27: Hryniv (2005) presented an example of a locally compact topological semigroup (S, τS) and a closed ideal I such that S/I is not a topological semigroup. Therefore by the above proposition, for the topological semigroup (S, τS ) which is presented (Hryniv, 2005), ρI is a topological S-act congruence however it is not a topological semigroup congruence.
Up to now, for a topological S-act (A, τA ), we prove present results by putting some conditions on (A, τA ) or (S, τS), or by putting some conditions on Y. In the next proposition, we put a condition on the lattice τA ∩ LY.
Proposition 28: Let Y≤A be a closed subact of (A, τA) such that there exists a minimum open subset which contains Y. Then ρY is a topological congruence if and only if the minimum open set which contains Y is a subact.
Proof: (Z) suppose that ρY is a topological congruence. So by Proposition 17, for any arbitrary aεY, sεS and minimum open set O which contains Y, there is an open set Va⊆ O which contains Y and an open set Ws around s such that saεWs ·Va⊆ O. Since O is the minimum open set, Va= O. Therefore, we have:
∀sεS, s· O⊆ O⇒S ·O⊆ O |
(⇒) Again, we use Proposition 17. Suppose that we are given aεY, sεS and an open set U which contains Y and saεU. Since, there exists a minimum open set O⊆ U which is a subact of A and contains Y, we have saεS· O⊆ O⊆ U. So ρY is a topological congruence.
Corollary 29: Let (A, τA ) be a topological S-act and Y be a clopen subact. Then ρY is a topological congruence.
ACKNOWLEDGMENTS
The author gratefully acknowledges his supervisor, Professor Ebrahimi and his advisor Professor Mahmoudi for their guidance and kindness. Also he is grateful to Professor Gutik, for his fruitful communications and helps.
REFERENCES
- Berglund, J.F. and K.H. Hofmann, 1967. Compact Semitopological Semigroups and Weakly Almost Periodic Functions. 1st Edn., Springer-Verlag, Berlin, New York, ISBN-10: 3540039139, pp: 170.
Direct Link - Berglund, J.F., D.J. Hugo and M. Paul, 1989. Analysis on Semigroups. Function Spaces, Compactifications, Representations, Canadian Mathematical Society Series of Monographs and Advanced Texts. A Wiley-Interscience Publication, John Wiley and Sons, Inc., New York, ISBN-10: 0471612081, pp: 334.
Direct Link - Burris, S. and H.P. Sankappanavar, 1981. A Course in Universal Algebra, Graduate Texts in Mathematics. 1st Edn., Springer-Verlag, New York, Berlin, ISBN-10: 0387905782, pp: 276.
Direct Link - Gonzalez, G., 2001. Closed congruences on semigroups. Divulgaciones Matematicas, 9: 103-107.
Direct Link - Hryniv, O., 2005. Quotient topologies on topological semilattices. Mat. Stud., 23: 136-142.
Direct Link - Kilp, M., U. Knauer and A.V. Mikhalev, 2000. Monoids Acts and Categories: with Applications to Wreath Products and Graphs, Expositions in Mathematics. Vol. 29, Walter de Gruyter, Berlin, New York, ISBN-10: 3110152487, pp: 529.
Direct Link - Lawson, J. and A. Lisan, 1994. Flows, congruences and factorizations. Topology Appl., 58: 35-46.
CrossRef - Wolfgang, R., 1984. Compact Semitopological Semigroups: An Intrinsic Theory. Lecture Notes in Mathematics. Springer-Verlag, Berlin, ISBN-10: 0387133879, pp: 260.
Direct Link








