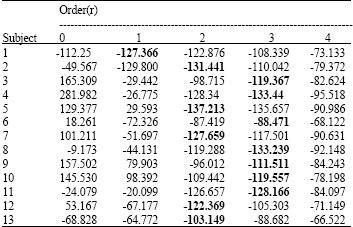
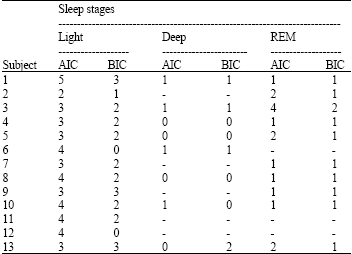
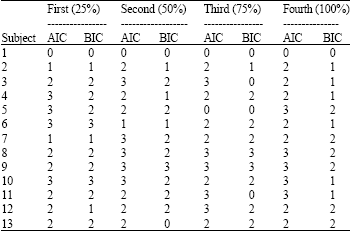
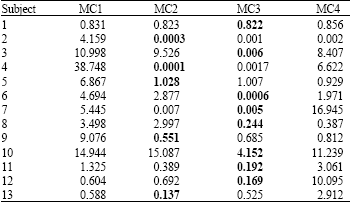
Research Article
Statistical Model of the Occurrence of Sleep Apnea
Department of Biomedical Science, Faculty of Allied Health Science, Universiti Kebangsaan Malaysia, Kuala Lumpur, Malaysia
A.A. Jemain
School of Mathematical Science, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Selangor, Malaysia
K. Ibrahim
School of Mathematical Science, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Selangor, Malaysia