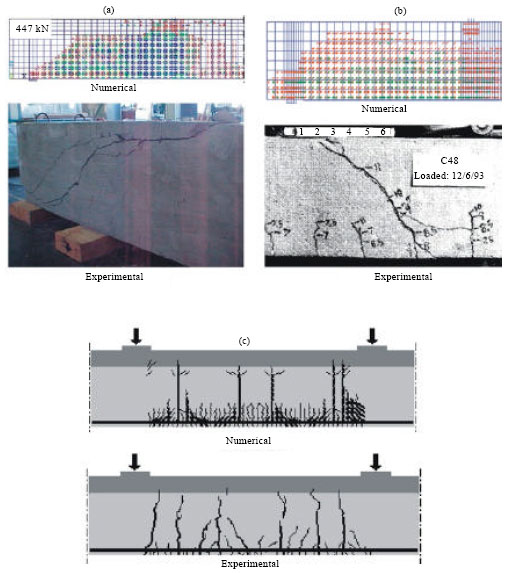
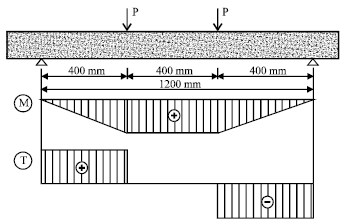
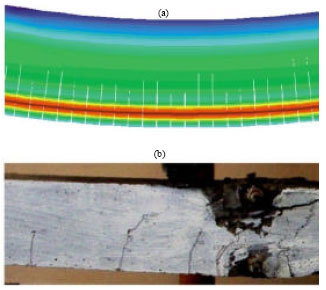
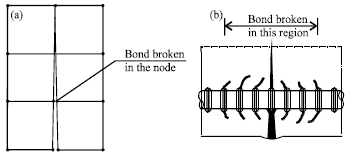
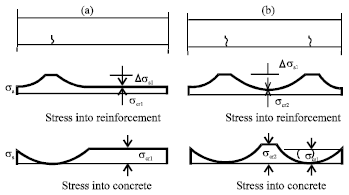
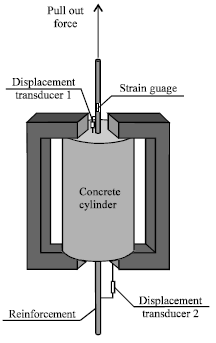
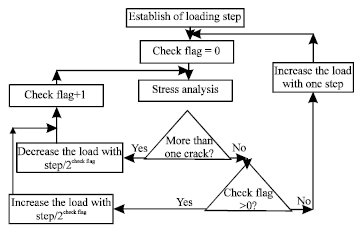
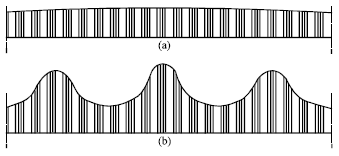
Research Article
Numerical Analysis of Bonding Between Concrete and Reinforcement using the Finite Element Method
Faculty of Civil Engineering and Building Services, 43 Dimitrie Mangeron Blvd., Iasi, 700050, Romania
Ioan Hirhui
Faculty of Civil Engineering and Building Services, 43 Dimitrie Mangeron Blvd., Iasi, 700050, Romania
Bogdan Rosca
Faculty of Civil Engineering and Building Services, 43 Dimitrie Mangeron Blvd., Iasi, 700050, Romania