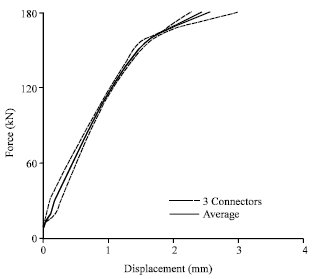
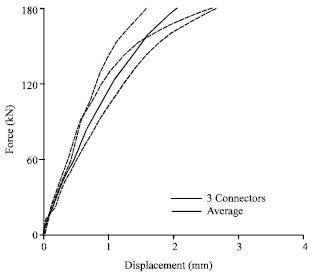
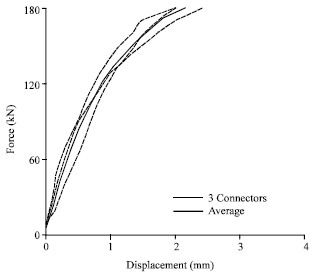
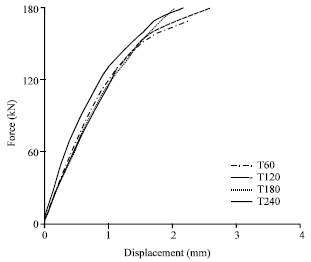
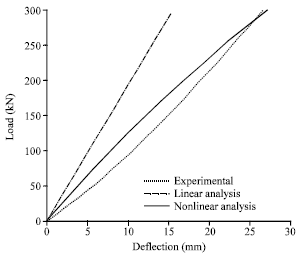
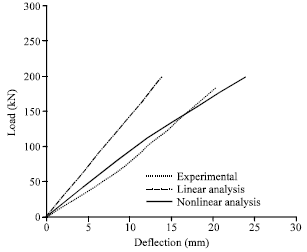
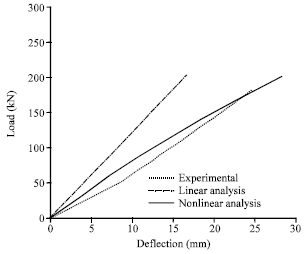
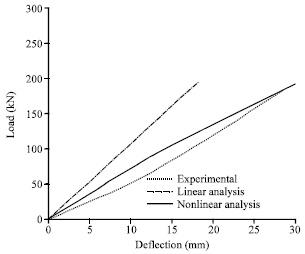
Research Article
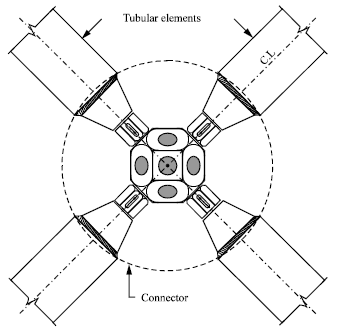
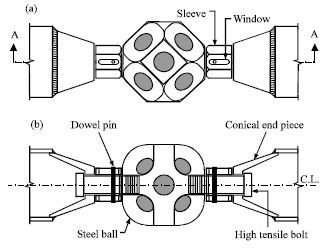
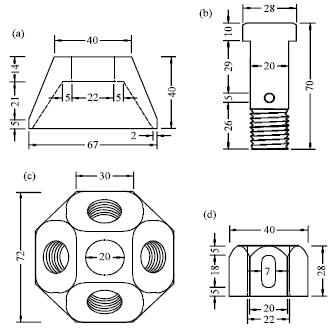
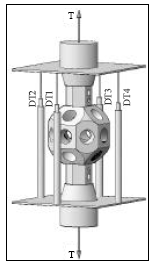
Tensile Stiffness of MERO-Type Connector Regarding Bolt Tightness
Department of Civil Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran
M.R. Davoodi
Department of Civil Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran
S.A. Mostafavian
Department of Civil Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran