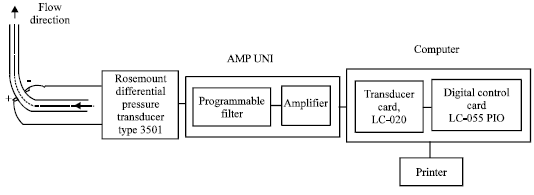
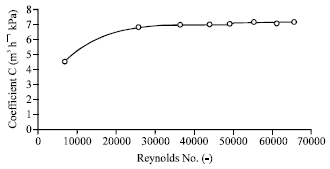
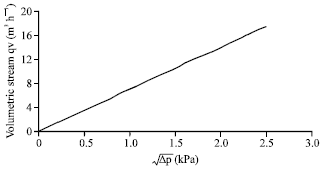
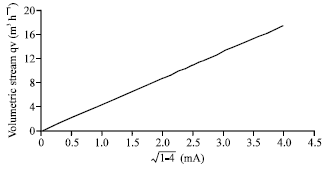
Research Article
Measurement of Water Stream Flowing to Steam Condenser in Condensing Power Plant
Tafila Technical University, Jordan
K. AlQdah
Tafila Technical University, Jordan
A. Andruszkiewicz
Wroclaw University of Technology, W. Wyspianskiego 27, 50-370 Wroclaw, Poland
K. Kubas
Wroclaw University of Technology, W. Wyspianskiego 27, 50-370 Wroclaw, Poland
J. Gorecki
Wroclaw University of Technology, W. Wyspianskiego 27, 50-370 Wroclaw, Poland