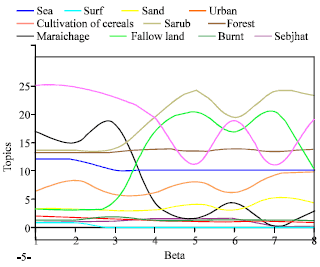
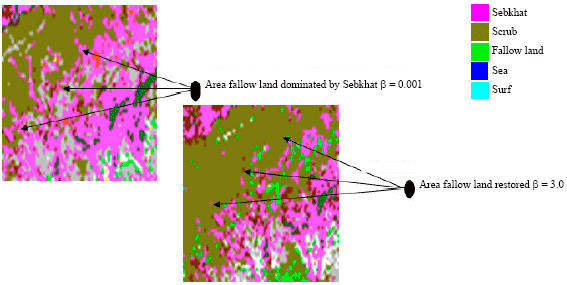
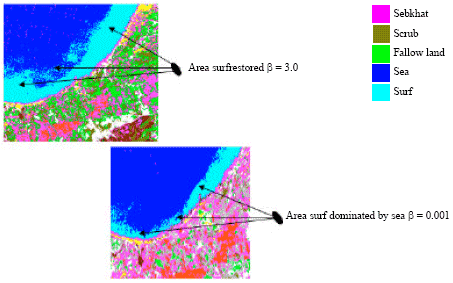
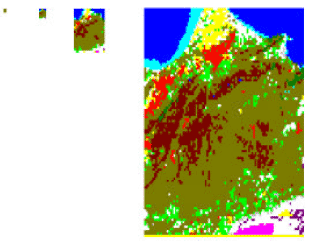
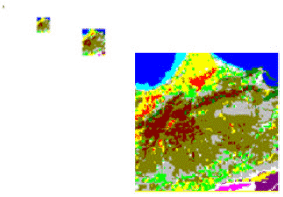
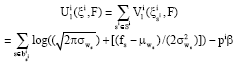Research Article
Classification of Remote Sensing Data with Markov Random Field
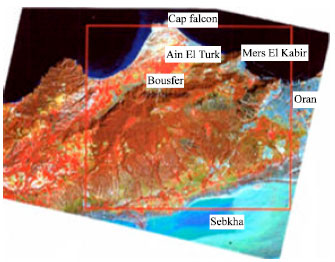
Laboratoire Signal Image Parole SIMPA, Department of Computer Science, Faculty of Science, University of Science and Technology of Oran, BP 1505 Oran El M�naouer, Algerie
R. Rabahi
Laboratoire Signal Image Parole SIMPA, Department of Computer Science, Faculty of Science, University of Science and Technology of Oran, BP 1505 Oran El M�naouer, Algerie