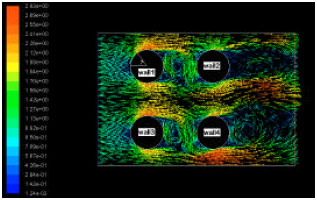
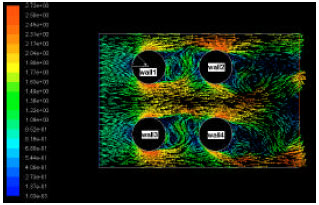
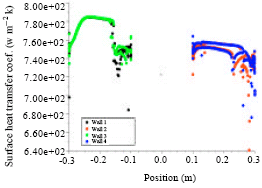
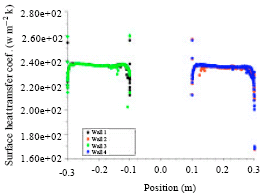
Research Article
Simulation of (EG+Al2O3) Nanofluid Through the Shell and Tube Heat Exchanger with Rectangular Arrangement of Tubes and Constant Heat Flux
Faculty of Mechanical Engineering, Sahand Tabriz University of Technology, Tabriz, Iran
R. Motallebzadeh
Faculty of Mechanical Engineering, Sahand Tabriz University of Technology, Tabriz, Iran
D. Jajali Vahid
Faculty of Mechanical Engineering, Sahand Tabriz University of Technology, Tabriz, Iran