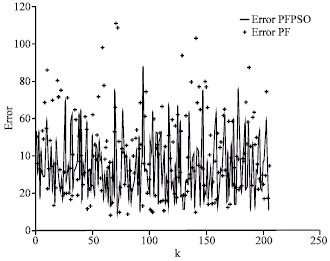
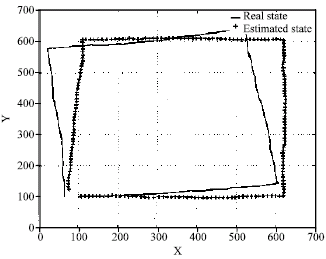
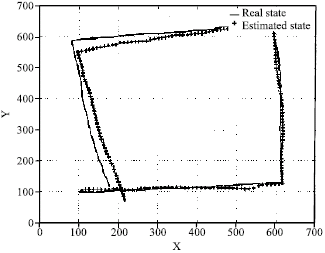
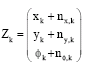Research Article
PFPSO: An Optimised Filtering Approach Based on Sampling
Laboratory of Simulations and Modelling of Industrial Systems, Department of Computer Science,Faculty of Science, University of Science and Technology of Oran Mohammed Boudiaf, USTO,P.O. Box 1505, El Menaour, Oran, Algeria
S. Hernane
Laboratory of Simulations and Modelling of Industrial Systems, Department of Computer Science,Faculty of Science, University of Science and Technology of Oran Mohammed Boudiaf, USTO,P.O. Box 1505, El Menaour, Oran, Algeria
M. Benyettou
Laboratory of Simulations and Modelling of Industrial Systems, Department of Computer Science,Faculty of Science, University of Science and Technology of Oran Mohammed Boudiaf, USTO,P.O. Box 1505, El Menaour, Oran, Algeria