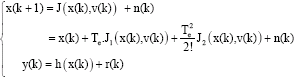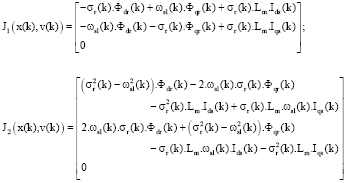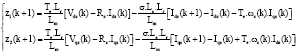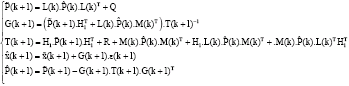Research Article
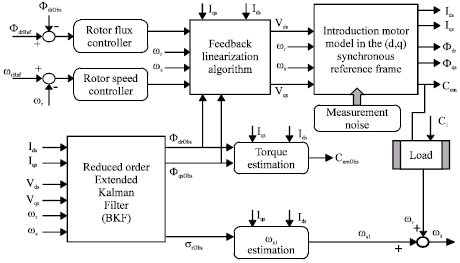
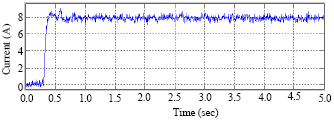
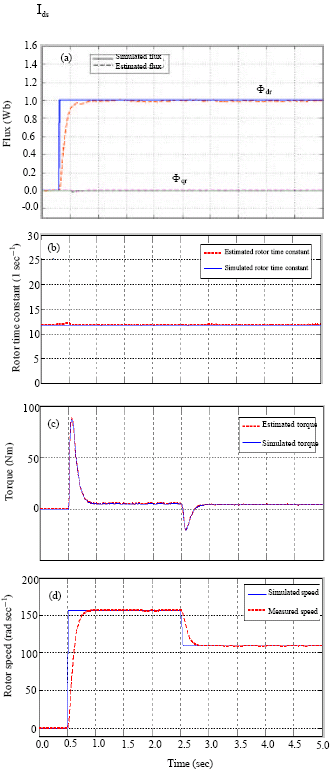
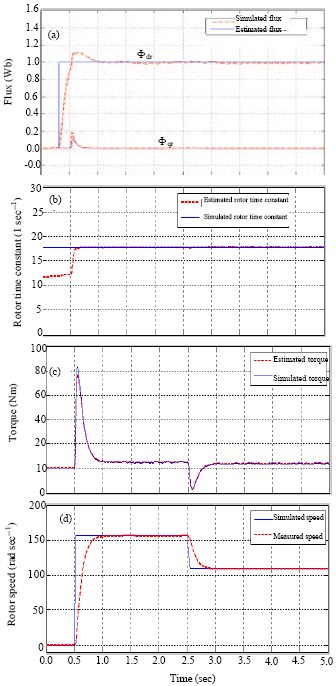
Sensorless Control of Induction Machines using a Reduced Order Extended Kalman Filter for Rotor Time Constant and Flux Estimation
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
Z. Yeo
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
M. Koffi
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
M.A. Kouacou
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
K.E. Ali
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire