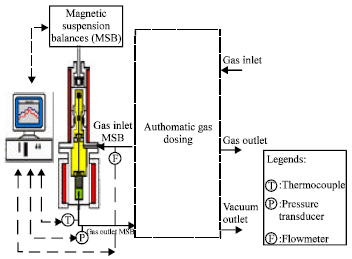
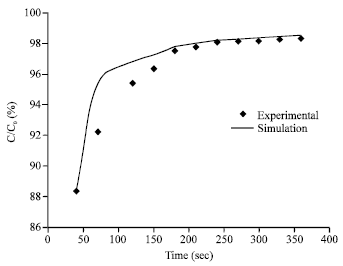
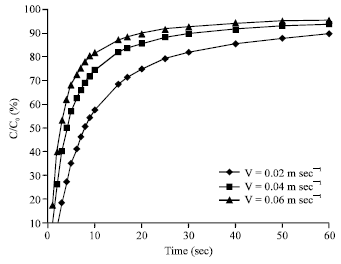
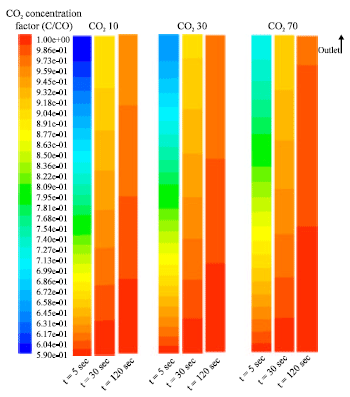
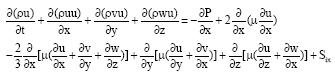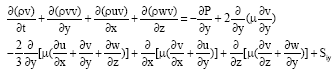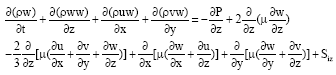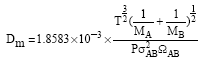Research Article
Modeling and Simulation of Fixed Bed Adsorption Column using Integrated CFD Approach
Department of Chemical Engineering, Universiti Teknologi PETRONAS 31750, Tronoh, Malaysia
K.K. Lau
Department of Chemical Engineering, Universiti Teknologi PETRONAS 31750, Tronoh, Malaysia
A.M. Shariff
Department of Chemical Engineering, Universiti Teknologi PETRONAS 31750, Tronoh, Malaysia