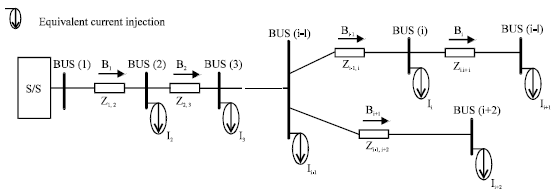
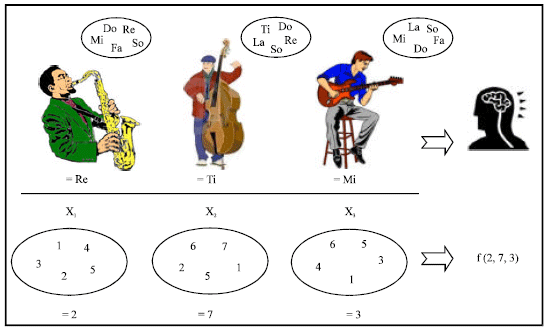
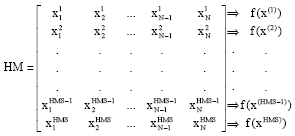
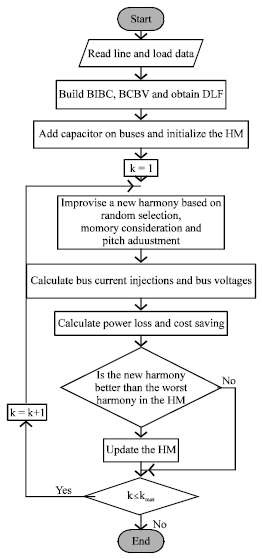
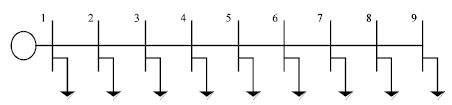
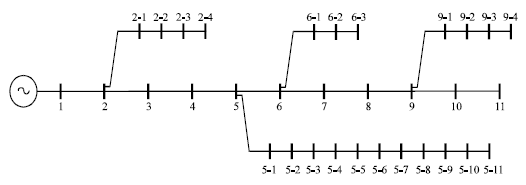
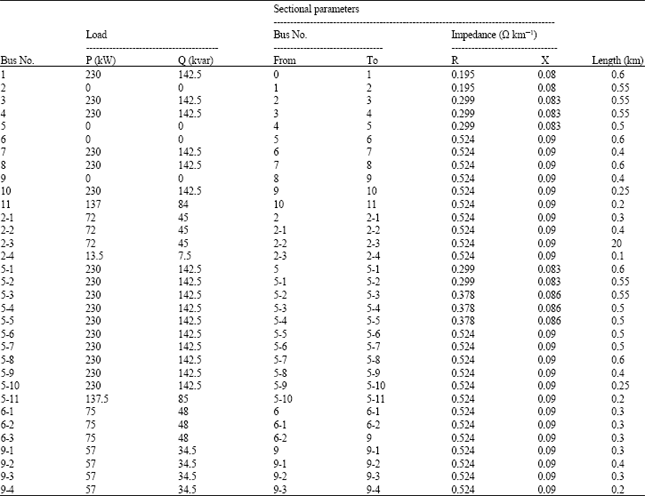
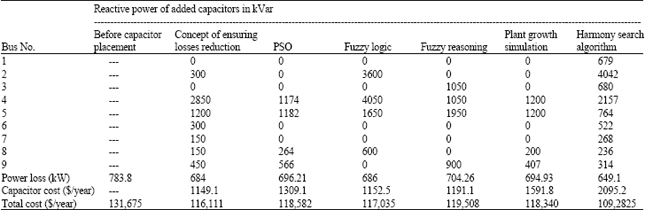
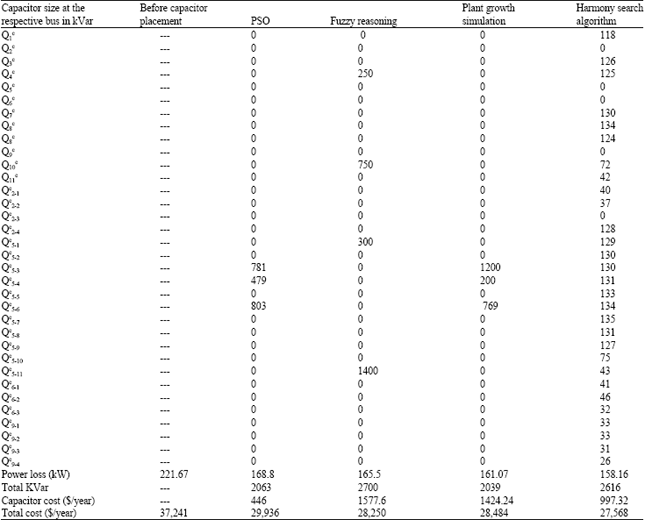
Research Article
Optimal Capacitor Placement in a Radial Distribution System using Harmony Search Algorithm
Department of Electrical, Electronic and Systems Engineering, Universiti Kebangsaan Malaysia, Bangi, 43600, Selangor, Malaysia
A. Mohamed
Department of Electrical, Electronic and Systems Engineering, Universiti Kebangsaan Malaysia, Bangi, 43600, Selangor, Malaysia
H. Shareef
Department of Electrical, Electronic and Systems Engineering, Universiti Kebangsaan Malaysia, Bangi, 43600, Selangor, Malaysia