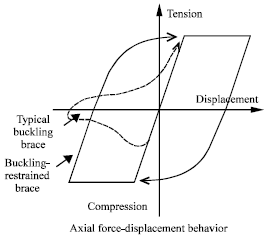
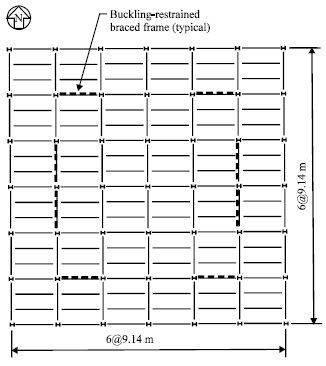
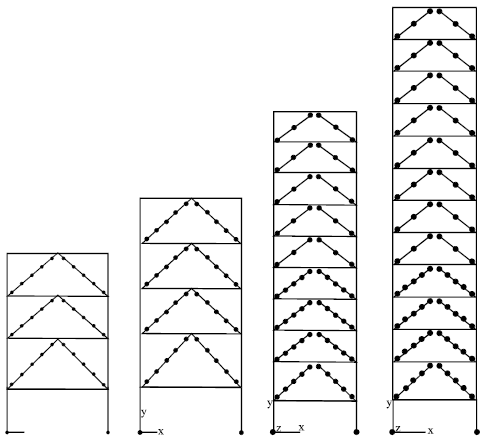
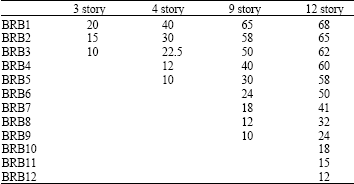
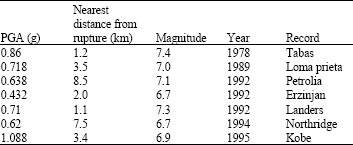
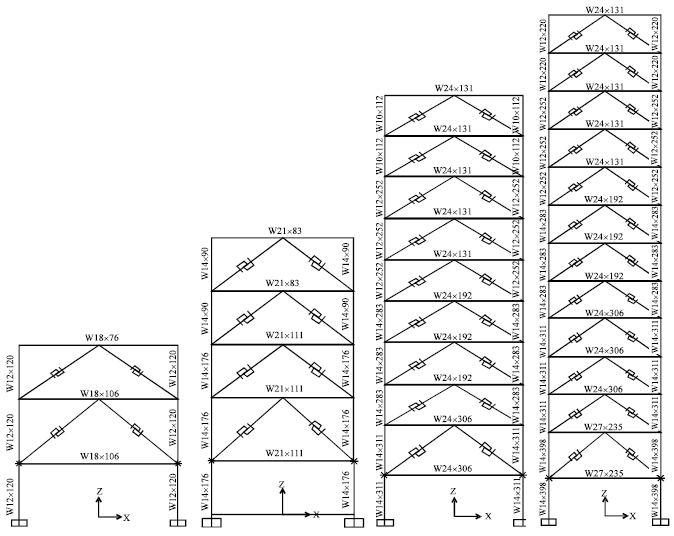
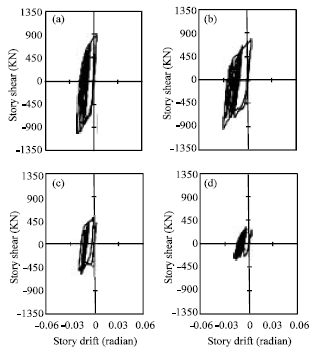
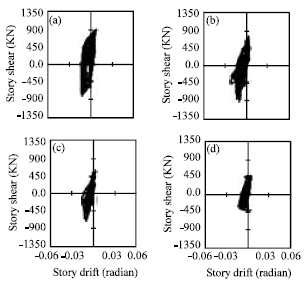
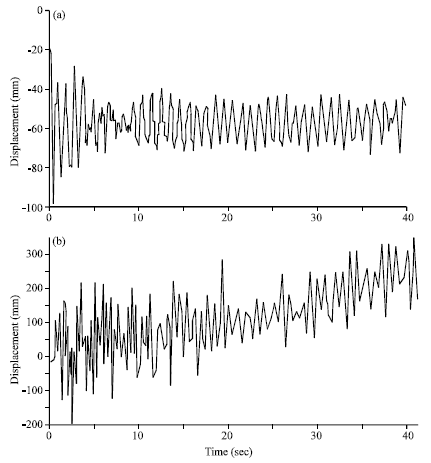
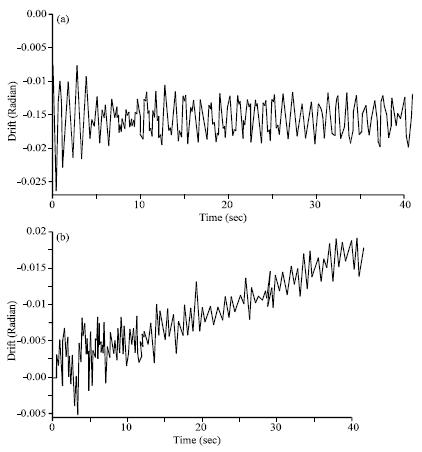
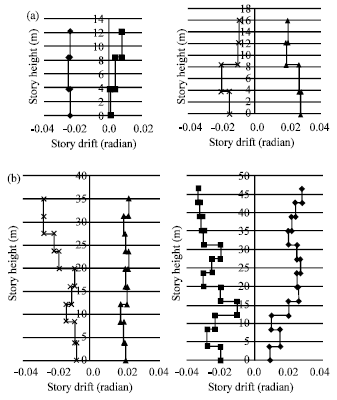
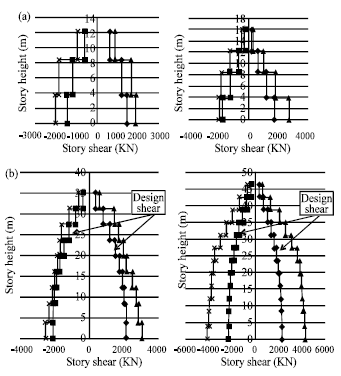
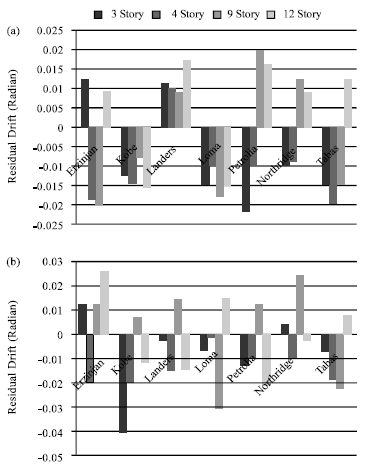
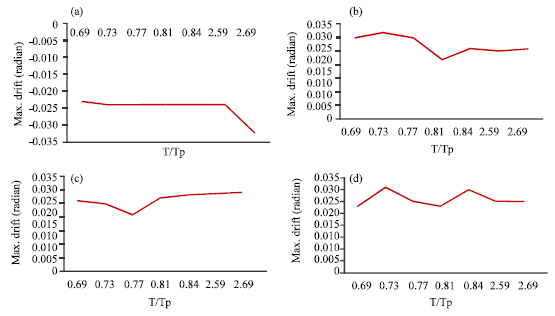
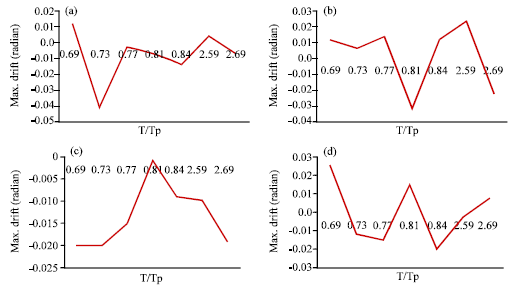
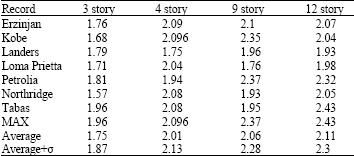
Research Article
Seismic Response of Buckling Restrained Braced Frames under Near Fault Ground Motions
Department of Structural Engineering, School of Civil Engineering, University of Tabriz, Tabriz, Iran
A. Jalali
Department of Structural Engineering, School of Civil Engineering, University of Tabriz, Tabriz, Iran
Y. Yasrebinia
Department of Structural Engineering, School of Civil Engineering, University of Tabriz, Tabriz, Iran