Research Article
Stochastic Programming with Tractable Meanb-risk Objectives for Refinery Planning under Uncertainty
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Stochastic programming has emerged as one of the most prominent operation research models for optimization involving uncertainty. Refinery planning problems are subject to uncertainty in many factors, which primarily includes fluctuations in prices of crude oil and saleable products, market demand for products and production yields. The risk terms in Khor et al. (2008) are handled using the metric mean-absolute deviation. After obtaining the first model with MAD as risk measurement, the second model is developed in which the risk terms are performed by CVaR. A comparison is performed between the two models to assess which of these two risk measures is superior, both computationally and conceptually, in capturing the economic and operating risk in the planning of a refinery. However, there are large numbers of scenarios that create difficulty to handle various circumstances. For example, there may be more than thousands of cases happening. It is hard to predict and control numerous scenarios. Therefore, it is necessary to find the minimum number of scenarios to capture all the circumstances. Monte Carlo simulation approach based on the Sample Average Approximation (SAA) technique is applied in this work to generate the minimum number of scenarios which present for thousands cases. The two-stage stochastic program with risk management as presented by Khor et al. (2008) is formulated as:
| (1) |
where, E[z0] is the expectation of the original objective function z0 with random price coefficients; θ1 and θ3 are weights representing the risk factors; V(z0) is the sampling variance of z0; Es is the expected recourse penalty and W is the MAD-based risk measure. In this work, we extend model Eq. 1 by considering MAD as the risk measure in place of variance. Further, we investigate the viability of the risk measure Conditional Value-at-Risk (CVaR), which has gained wide attention in computational finance, within the domain of refinery planning. All the uncertain parameters are assumed to be discrete random variables.
MONTE CARLO SIMULATION APPROACH BASED ON SAMPLE AVERAGE APPROXIMATION (SAA) METHOD
In this study, we adopt the Monte Carlo simulation approach for scenario generation based on the Sample Average Approximation (SAA) method (You et al., 2009; Shapiro, 2000; Shapiro and Homem-de-Mello, 1998). The procedure involved is as follows:
| • | Step 1: A relatively small number of scenarios (for example, 50 scenarios) with their associated probabilities are randomly and independently generated for the uncertain parameters of prices, demands and yields. This is accomplished by employing the Monte Carlo simulation approach based on the SAA technique. (This data is otherwise obtained from plant historical data.) The resulting stochastic model (a linear program) with the objective function given in Eq. 2 is solved to determine the optimal stochastic profit with its corresponding material flowrates: |
| (2) |
where,
and
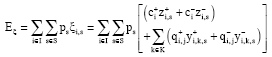 |
| • | Step 2: The Monte Carlo sampling variance estimator is determined using the optimal stochastic profit and flowrates computed in step 1. |
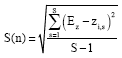 | (3) |
where,
| • | Step 3: The lower- and upper-confidence limits of the 95% confidence interval H of 1-α are computed as follows: |
| (4) |
| • | Step 4: The minimum number of scenarios N that is theoretically required to obtain an optimal solution is determined using the relation below: |
| (5) |
where, the standard normal random variable zα/2 = 1.96 at confidence interval (1-α) = 95%.
MODEL FORMULATION OF STOCHASTIC REFINERY PLANNING MODEL WITH MEAN-ABSOLUTE DEVIATION (MAD) AS RISK MEASURE
The risk metric Mean-Absolute Deviation (MAD) is employed as a measure of deviation from the expected profit (Konno and Yamazaki, 1991). It is defined as follows:
| (6) |
In this study, the rate of return R in Eq. 6 refers to unit cost of materials (crude oil and refinery products) and the amount of money xj invested in an asset j refers to the refinery production amount. Therefore, the formulation of the MAD-based risk measure for price uncertainty becomes:
| (7) |
while for demands and yields uncertainty, it is given by:
| (8) |
FORMULATION OF STOCHASTIC REFINERY PLANNING MODEL WITH CONDITIONAL VALUE-AT-RISK (CVAR) AS RISK MEASURE
CvaR, also termed as mean excess loss, mean shortfall or tail VaR, is a risk assessment technique that is originally intended to be employed for reducing the probability that an investment portfolio will incur high losses. It offers the advantage of a linear programming formulation for determining the optimal solution of financial planning problems that explicitly minimizes loss or risk. CVaR is performed by taking the likelihood (at a specific confidence level, e.g., 0.95 or 0.99) that a specific loss will exceed the metric known as Value-at-Risk (VaR). From a mathematical point of view, CVaR is derived by taking a weighted average between VaR and the losses exceeding VaR. For a discrete probability distribution function, CVaR can be defined as follows (Rockafellar and Uryasev, 2002, 2000):
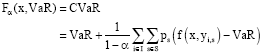 | (9) |
Using CVaR as the risk metric yields the following form of the objective function:
| (10) |
where, CVaRz0 is the risk measure imposed by the recourse costs to handle price uncertainty.
| (11) |
where, CvaRξ is the risk measure imposed by the recourse costs to handle uncertainty in demands and yields.
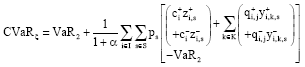 | (12) |
Substituting Eq. 10 and 11 into 9, we obtain a two-stage stochastic programming model with meanBrisk objective in which the risk measures are assessed by CVaR.
NUMERICAL EXPERIMENTS
We illustrate the risk modeling approach proposed in this paper on the numerical example taken from Khor et al. (2008) and provide major details on the implementation using GAMS/CONOPT3.
Solving two-stage stochastic program with MAD as risk measure: The expectation of the objective function value is given by the original objective function itself: The corresponding expression for expected profit is formulated for the 13 scenarios that has been randomly generated.
Solving two-stage stochastic program with CVaR as risk measure: The following is the procedure for developing a loss distribution in order to determine the value for the parameter VaR.
| • | Step 1: The objective value of deterministic profit for each of the 13 scenarios is computed (i.e., multiplication of flowrate and the corresponding price per unit flowrate) |
| • | Step 2: The probability of each scenario is randomly generated using Monte Carlo simulation based on pseudorandom number generation |
| • | Step 3: The computed values in step 1 are sorted in ascending order |
| • | Step 4: The plot of cumulative distribution function against the sorted deterministic profit values is developed to obtain a representation of the loss distribution. At confidence interval of (1-α) = 0.95, we can read off the value of VaR from the loss distribution plot, as depicted in Fig. 1 and 2, which represents the penalty for uncertainty in prices and in both demands and yields, respectively. The computational statistics and a summary of the main computational results are provided in Table 1 and 2, respectively |
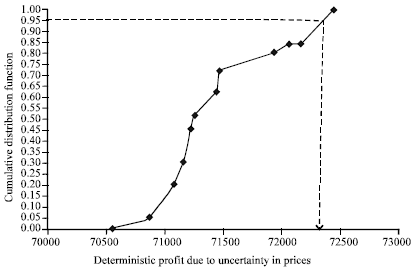 | |
| Fig. 1: | Loss distribution to determine VaR1 |
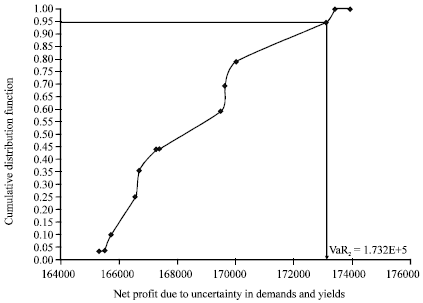 | |
| Fig. 2: | Loss distribution to determine VaR2 |
| Table 1: | Summary of computational results |
 | |
| Table 2: | Computational statistics of GAMS implementation for determining optimal solutions of MAD- and CVaR-based meanBrisk stochastic program |
 | |
In this study, we have proposed a stochastic nonlinear programming model with recourse that incorporates the risk metrics of MAD and CVaR to handle economic and operational risk management in refinery planning problems under uncertainty in prices, demands and yields. The model involves the application of Monte Carlo simulation approach based on the Sample Average Approximation (SAA) method to determine the minimum number of scenarios required to obtain an optimal solution. Therefore, the main idea of this study is to combine the scenario reduction technique of SAA with the novel application of the computationally-attractive risk metric CvaR to refinery planning problems. The model is applied to a representative refinery planning problem in the literature to illustrate its computational performance.
ACKNOWLEDGMENTS
Author is grateful to Universiti Teknologi PETRONAS for the full support of this study and acknowledges Thi Huynh Nga Nguyen, his undergraduate research assistant, for her contribution in the computational work.